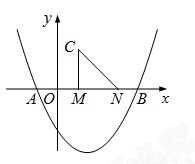题目内容
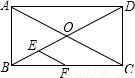
如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,点E、F分别是BO、BC的中点,若AB=6cm,则△BEF的周长为
6+3 .
.
【解析】
试题分析:根据矩形的性质,可以得到△AOB是等边三角形,则可以求得OA的长,进而求得AC的长,再利用三角形中位线定理得出△BEF的周长为△BOC周长的一半求出即可.
试题解析:∵矩形ABCD,OA=OB
又∵∠AOB=60°
∴△AOB是等边三角形.
∴OA=AB=6cm,
∴OC=OB=6cm,AC=12cm,
∴BC= =6
=6 (cm),
(cm),
∵点E、F分别是BO、BC的中点,
∴EF= CO,BE=
CO,BE= BO,BF=
BO,BF= BC,
BC,
∴△BEF的周长为△BOC周长的一半为:
 (6+6+6
(6+6+6 )=6+3
)=6+3 .
.
考点:1.矩形的性质;2.等边三角形的判定与性质;3.三角形中位线定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 m次,小货车每天比原计划多跑m次,一天刚好运送了帐篷14400顶,求m的值.
m次,小货车每天比原计划多跑m次,一天刚好运送了帐篷14400顶,求m的值.


 C.
C. D.
D.
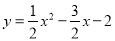 的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.