题目内容
6. 如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.
如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O,若∠ABC=40°,∠ACB=60°,求∠BOC的大小.
分析 先根据三角形内角和定理求出∠ABC的度数,再由角平分线的性质得出∠OBC与∠OCB的度数,进而可得出结论.
解答 解:∵在△ABC中,∠ABC=40°,∠ACB=60°,
∴∠ABC=180°-40°-60°=80°.
∵∠ABC,∠ACB的平分线BD,CE相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC=40°,∠OCB=$\frac{1}{2}$∠ACB=30°,
∴∠BOC=180°-40°-30°=110°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
16.若分式$\frac{2x+1}{{x}^{2}}$的值为正,则x的取值范围是( )
| A. | x>0 | B. | x>-$\frac{1}{2}$ | C. | x≠-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠0 |
13.已知二次函数y=ax2+bx+1,若当x=1时,y=0;当x=-1时,y=4,则a、b的值分别为( )
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
18.小芳有两根长度为4cm和9cm的木条,他想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择的木条的长度只能是( )
| A. | 5 cm | B. | 3 cm | C. | 17 cm | D. | 12 cm |
16. 如图,AC、BD交于E点,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
如图,AC、BD交于E点,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
 如图,AC、BD交于E点,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )
如图,AC、BD交于E点,AC=BD,AE=BE,∠B=35°,∠1=95°,则∠D的度数是( )| A. | 60° | B. | 35° | C. | 50° | D. | 75° |
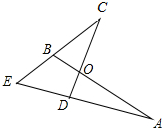 如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,AB=CD,你能说明∠A=∠C吗?点O在∠AEC的平分线上吗?
如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,AB=CD,你能说明∠A=∠C吗?点O在∠AEC的平分线上吗?