题目内容
8．
如图，MN是⊙O的直径，矩形ABCD的顶点A、D在MN上，顶点B、C在⊙O上，若⊙O的半径为5，AB=4，则BC边的长为6．
分析 作OE⊥BC于E，根据垂径定理得到BE=EC，根据勾股定理求出BE的长，得到答案．
解答 解：
作OE⊥BC于E，
则BE=EC，
由题意得，四边形ABEO为矩形，
∴OE=AB=4，
由勾股定理得，BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=3，
则BC=2BE=6，
故答案为：6．
点评 本题考查的是垂径定理、勾股定理、矩形的性质的应用，掌握相关的性质定理是解题的关键．
练习册系列答案
活力课时同步练习册系列答案
相关题目
如图，在△ABC中，∠ABC=90°，BD为AC边的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AB=12，BC=5，则四边形BDFG的周长为26．
如图，按虚线剪去长方形纸片的相邻两个角，并使∠1=120°，AB⊥BC，那么∠2的度数为150°．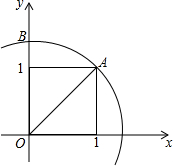
如图，平面直角坐标中，以x轴上一个单位长度为边长画一个正方形，以原点为圆心，正方形的对角线OA为半径画弧，与y轴正半轴的交点B表示的坐标是（0，$\sqrt{2}$）．
如图，某工厂师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面，且要使大正方形的边长比小正方形的边长大1m，则裁剪后剩下的阴影部分的面积为2m2．
如图，10块相同的长方形墙砖拼成一个长方形，设长方形墙砖的长为x厘米，则x=45厘米．