题目内容
15.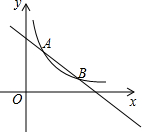 如图,在平面直角坐标系中,一次函数的图象y1=kx+b与反比例函数y2=$\frac{n}{x}$的图象交于点A(1,5)和点B(m,1).
如图,在平面直角坐标系中,一次函数的图象y1=kx+b与反比例函数y2=$\frac{n}{x}$的图象交于点A(1,5)和点B(m,1).(1)求m的值和反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式$\frac{n}{x}$≥kx+b的解集;
(3)若经过点B的抛物线的顶点为A,求该抛物线的解析式.
分析 (1)利用待定系数法求得反比例函数解析式,然后把B的坐标代入求得m的值;
(2)不等式$\frac{n}{x}$≥kx+b的解集就是反比例函数的图象在一次函数的图象的交点以及反比例函数图象在上方时对应的x的范围;
(3)利用待定系数法即可求得二次函数的解析式.
解答 解:(1)∵反比例函数${y_2}=\frac{n}{x}$的图象交于点A(1,5),
∴5=n,即n=5,
∴反比例函数的解析式是y=$\frac{5}{x}$,
∵点B(m,1)在双曲线上.∴1=$\frac{5}{m}$,
∴m=5,
∴B(5,1);
(2)不等式$\frac{n}{x}$≥kx+b的解集为0<x≤1或x≥5;
(3)∵抛物线的顶点为A(1,5),
∴设抛物线的解析式为y=a(x-1)2+5,
∵抛物线经过B(5,1),
∴1=a(5-1)2+5,解得a=-$\frac{1}{4}$.
∴二次函数的解析式是y=-$\frac{1}{4}$(x-1)2+5.
点评 本题考查了二次函数与一次函数的图象的交点以及待定系数法求二次函数的解析式,根据特点正确设出二次函数的解析式是关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.点A在第二象限,且到x轴的距离为2,到y轴的距离为3,则点A的坐标是( )
| A. | (-2,3) | B. | (-3,2) | C. | (3,-2) | D. | (2,-3) |
3.不等式组$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}>2-x}\end{array}\right.$的解集是( )
| A. | x>$\frac{4}{5}$ | B. | x≥8 | C. | $\frac{4}{5}$<x≤8 | D. | 无解 |
10.一次数学作业共有10道题目,某小组8位学生做对题目数的情况如下表:
那么这8位学生做对题目数的众数和中位数分别是( )
| 做对题目数 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 1 | 2 | 3 | 1 |
| A. | 9和8 | B. | 9和8.5 | C. | 3和2 | D. | 3和1 |
20.商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如表所示:
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 2 | 6 | 11 | 15 | 7 | 3 | 4 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
7.人体血液中,红细胞的直径约为0.000 007 7m.用科学记数法表示0.000 007 7m是( )
| A. | 0.77×10-5 | B. | 7.7×10-5 | C. | 7.7×10-6 | D. | 77×10-7 |
4.已知样本数据1,2,3,3,4,5,这组数据的中位数是( )
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
5.已知点P1(x1,y1)、P2(x2,y2)在双曲线y=$\frac{3}{x}$上,下列说法中,正确的是( )
| A. | 若x1>x2,则y1>y2 | B. | 若x1>x2,则y1<y2 | ||
| C. | 若x1>x2>0,则y1>y2 | D. | 若x1>x2>0,则y1<y2 |