题目内容
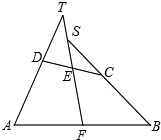 如图,在四边形ABCD中,AD=BC,E、F分别是CD、AB的中点,直线EF分别交BC、AD的延长线于S、T两点,求证:∠ATF=∠BSF.
如图,在四边形ABCD中,AD=BC,E、F分别是CD、AB的中点,直线EF分别交BC、AD的延长线于S、T两点,求证:∠ATF=∠BSF.考点:三角形中位线定理
专题:证明题
分析:连接AC,取AC的中点H,连接EH、FH,根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥AD,EH=
AD,FH∥BC,FH=
BC,然后求出EH=FH,根据等边对等角可得∠EFH=∠FEH,再根据两直线平行,同位角相等可得∠ATF=∠FEH,两直线平行,内错角相等可得∠BSF=∠EFH,然后等量代换即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
解答: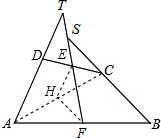 证明:如图,连接AC,取AC的中点H,连接EH、FH,
证明:如图,连接AC,取AC的中点H,连接EH、FH,
∵E、F分别是CD、AB的中点,
∴EH、FH分别是△ACD和△ABC的中位线,
∴EH∥AD,EH=
AD,FH∥BC,FH=
BC,
∵AD=BC,
∴EH=FH,
∴∠EFH=∠FEH,
又∵EH∥AD,FH∥BC,
∴∠ATF=∠FEH,∠BSF=∠EFH,
∴∠ATF=∠BSF.
 证明:如图,连接AC,取AC的中点H,连接EH、FH,
证明:如图,连接AC,取AC的中点H,连接EH、FH,∵E、F分别是CD、AB的中点,
∴EH、FH分别是△ACD和△ABC的中位线,
∴EH∥AD,EH=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=BC,
∴EH=FH,
∴∠EFH=∠FEH,
又∵EH∥AD,FH∥BC,
∴∠ATF=∠FEH,∠BSF=∠EFH,
∴∠ATF=∠BSF.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行线的性质,等边对等角的性质,熟记各性质并作辅助线,考虑利用三角形的中位线定理是解题的关键.

练习册系列答案
相关题目