题目内容
18.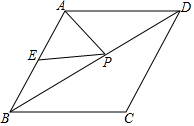 如图,已知菱形ABCD的周长为16,面积为8$\sqrt{3}$,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2$\sqrt{3}$.
如图,已知菱形ABCD的周长为16,面积为8$\sqrt{3}$,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为2$\sqrt{3}$.
分析 如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.首先证明E′与E重合,因为A、C关于BD对称,所以当P与P′重合时,PA′+P′E的值最小,由此求出CE即可解决问题.
解答 解:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8$\sqrt{3}$,
∴AB=BC=4,AB•CE′=8$\sqrt{3}$,
∴CE′=2$\sqrt{3}$,
在Rt△BCE′中,BE′=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,PA′+P′E的值最小,最小值为CE的长=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 本题考查轴对称-最短问题、菱形的性质等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明CE是△ABC的高,学会利用对称解决最短问题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
9.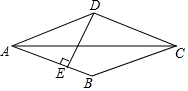 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )| A. | $\frac{75}{13}$ | B. | $\frac{96}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{144}{13}$ |
10.在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
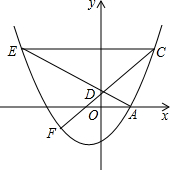 如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.
如图,抛物线y=$\frac{1}{4}$x2+$\frac{1}{2}$x-2与x轴正半轴交于点A,点D(0,m)为y轴正半轴上一点,连结AD并延长交抛物线于点E,若点C(4,n)在抛物线上,且CE∥x轴.