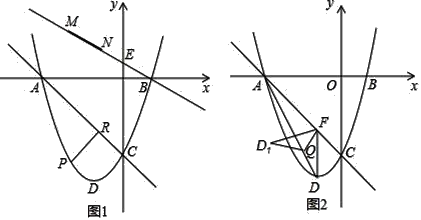
ƒøƒĞ»ı
°æƒø°ø»Ù»Œ“‚“ª∏ˆ¥˙ ˝ Ω£¨‘Ğ∏¯∂®µƒ∑∂ŒßƒĞ«Ûµ√µƒ◊Ó÷µ«°∫√“≤‘Ğ∏√∑∂ŒßƒĞ£¨‘Ú≥∆’‚∏ˆ¥˙ ˝ Ω «’‚∏ˆ∑∂Œßµƒ°∞”—∫√¥˙ ˝ Ω°±£Æ¿˝»Á£∫πÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() £¨µ±
£¨µ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() ‘Ğ
‘Ğ![]() ±”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™1£ª‘Ğ
±”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™1£ª‘Ğ![]() ±”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0£¨¥À ±◊Ó÷µ1£¨0æ˘‘Ğ
±”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0£¨¥À ±◊Ó÷µ1£¨0æ˘‘Ğ![]() £®∫¨∂Àµ„£©’‚∏ˆ∑∂ŒßƒĞ£¨‘Ú≥∆¥˙ ˝ Ω
£®∫¨∂Àµ„£©’‚∏ˆ∑∂ŒßƒĞ£¨‘Ú≥∆¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
£®1£©»Ùπÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() £¨µ±
£¨µ±![]() ±£¨»°µ√µƒ◊Ó¥Û÷µŒ™________£ª◊Ó–°÷µŒ™________£ª¥˙ ˝ Ω
±£¨»°µ√µƒ◊Ó¥Û÷µŒ™________£ª◊Ó–°÷µŒ™________£ª¥˙ ˝ Ω![]() ________£®ÃÓ°∞ «°±ªÚ°∞≤ª «°±£©
________£®ÃÓ°∞ «°±ªÚ°∞≤ª «°±£©![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£ª
µƒ°∞”—∫√¥˙ ˝ Ω°±£ª
£®2£©“‘œ¬πÿ”Ğ![]() µƒ¥˙ ˝ Ω£¨ «
µƒ¥˙ ˝ Ω£¨ «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «________£ª
µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «________£ª
¢Ÿ![]() £ª¢Ğ
£ª¢Ğ![]() £ª¢ğ
£ª¢ğ![]() £ª
£ª
£®3£©»Ùπÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£¨‘Ú
µƒ°∞”—∫√¥˙ ˝ Ω°±£¨‘Ú![]() µƒ÷µ «________£ª
µƒ÷µ «________£ª
£®4£©»Ùπÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£¨«Û
µƒ°∞”—∫√¥˙ ˝ Ω°±£¨«Û![]() µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
°æ¥∞∏°ø£®1£©3£¨0£¨≤ª « £®2£©¢Ğ £®3£©![]() £®4£©
£®4£©![]() µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
°æΩ‚Œˆ°ø
£®1£©«Û≥ˆ¥˙ ˝ Ωµƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£¨‘Ÿ∏˘æı”—∫√¥˙ ˝ Ωµƒ∂®“ÂΩ¯––≈–∂œº¥ø…£ª
£®2£©∏˘æı”—∫√¥˙ ˝ Ωµƒ∂®“Â∂‘∏˜¥˙ ˝ ΩΩ¯––«ÛΩ‚º¥ø…£ª
£®3£©∑÷»˝÷÷«ÈøˆΩ¯––«ÛΩ‚£∫¢Ÿ![]() £ª¢Ğ
£ª¢Ğ![]() £ª¢ğ
£ª¢ğ![]() £¨º¥ø…«Û≥ˆmµƒ÷µ£ª
£¨º¥ø…«Û≥ˆmµƒ÷µ£ª
£®4£©∑÷»˝÷÷«ÈøˆΩ¯––«ÛΩ‚£∫¢Ÿ![]() £ª¢Ğ
£ª¢Ğ![]() £ª¢ğ
£ª¢ğ![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨º¥ø…«Û≥ˆ
£¨º¥ø…«Û≥ˆ![]() µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
µƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
£®1£©°ş![]()
°‡µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™0
°‡![]() £¨
£¨![]()
π ¥˙ ˝ Ω![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
£®2£©¢Ÿ°şµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™3£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-1£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-1£¨
°‡![]() £¨
£¨![]()
°‡![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
¢Ğ°şµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-2£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-2£¨
°‡![]() £¨
£¨![]()
°‡![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
¢ğ°şµ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™2£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
°‡![]() £¨
£¨![]()
°‡![]() ≤ª «
≤ª «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±£Æ
π «![]() µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «¢Ğ£Æ
µƒ°∞”—∫√¥˙ ˝ Ω°±µƒ «¢Ğ£Æ
£®3£©°şπÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±
µƒ°∞”—∫√¥˙ ˝ Ω°±
°‡∑÷“‘œ¬»˝÷÷«ÈøˆΩ¯––Ã÷¬ğ£∫
¢Ÿ![]()
![]()
°‡µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™4£ªµ±
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™4£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°‡![]()
°‡≤ª≥…¡¢
¢Ğ![]()
![]()
°‡![]() £¨
£¨![]()
°‡![]()
Ω‚µ√![]()
°‡µ±![]() ≥…¡¢
≥…¡¢
¢ğ![]()
![]()
°‡µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™-4£¨
°ş![]()
°‡≤ª≥…¡¢
π ![]() µƒ÷µ «
µƒ÷µ «![]() £Æ
£Æ
£®4£©°şπÿ”Ğ![]() µƒ¥˙ ˝ Ω
µƒ¥˙ ˝ Ω![]() «
«![]() µƒ°∞”—∫√¥˙ ˝ Ω°±
µƒ°∞”—∫√¥˙ ˝ Ω°±
°‡∑÷“‘œ¬»˝÷÷«ÈøˆΩ¯––Ã÷¬ğ
¢Ÿ![]()
µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°‡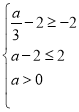
Ω‚µ√![]()
¢Ğ![]()
![]()
°ş![]()
°‡![]() ±≥…¡¢
±≥…¡¢
¢ğ![]()
µ±![]() ±£¨
±£¨![]() ”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™![]() £¨
£¨
°‡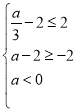
ŒŞΩ‚
°‡![]()
°‡![]() µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ
µƒ◊Ó¥Û÷µŒ™4∫Õ◊Ó–°÷µŒ™0£Æ