题目内容
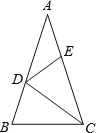
【题目】如图，在△ABC中，∠A=36°，AB=AC，CD是△ACB的角平分线．若在边AC上截取CE=CB，连接DE，则图中等腰三角形共有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
根据条件分别求出图中三角形的内角的度数，再根据等腰三角形的判定即可找出图中的等腰三角形.
解：∵AB=AC，∴△ABC是等腰三角形；
∵AB=AC，∠A=36°，∴∠B=∠ACB=72°．
∵CD是△ABC的角平分线，
∴∠ACD=∠DCB
∠ACB=36°，
∴∠A=∠ACD=36°，∴CD=AD，∴△ACD是等腰三角形；
在△BCD中，∵∠BDC=180°﹣∠B﹣∠BCD=180°﹣72°﹣36°=72°，
∴∠B=∠BDC=72°，∴DC=BC，∴△BCD是等腰三角形；
∵CE=CB，∴CD=CE，∴△CDE是等腰三角形；
∴∠CED=（180°﹣36°）÷2=72°，
∴∠ADE=∠CED﹣∠A=72°﹣36°=36°，
∴∠A=∠ADE，∴DE=AE，∴△ADE是等腰三角形；
∴图中的等腰三角形有5个．
故选D．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
