��Ŀ����
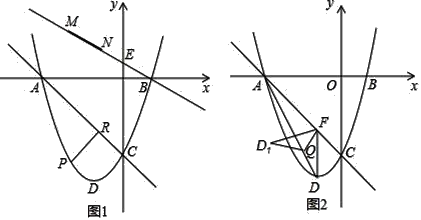
����Ŀ����ͼ1����֪������y=x2+2x��3��x���ཻ��A��B���㣬��y�ύ�ڵ�C��DΪ���㣮
��1����ֱ��AC�Ľ���ʽ�Ͷ���D�����ꣻ
��2����֪E��0�� ![]() ������P��ֱ��AC�·�����������һ���㣬��PR��AC�ڵ�R����PR���ʱ����һ����Ϊ
������P��ֱ��AC�·�����������һ���㣬��PR��AC�ڵ�R����PR���ʱ����һ����Ϊ![]() ���߶�MN����M�ڵ�N����ࣩ��ֱ��BE���ƶ�����β˳������A��M��N��P�����ı���AMNP��������ı���AMNP���ܳ���Сʱ��N�����ꣻ
���߶�MN����M�ڵ�N����ࣩ��ֱ��BE���ƶ�����β˳������A��M��N��P�����ı���AMNP��������ı���AMNP���ܳ���Сʱ��N�����ꣻ
��3����ͼ2������D��DF��y�ύֱ��AC�ڵ�F������AD��Q�����߶�AD��һ���㣬����DFQ��ֱ��FQ�۵�����D1FQ���Ƿ���ڵ�Qʹ����D1FQ����AFQ�ص����ֵ�ͼ����ֱ�������Σ������ڣ������AQ�ij����������ڣ���˵�����ɣ�
���𰸡���1��ֱ��AC�Ľ���ʽΪy=��x��3����D���꣨��1����4������2��N��0�� ![]() ������3��AQ�ij�Ϊ1+
������3��AQ�ij�Ϊ1+![]() ��
��![]() ��
��![]() ��
��
�������������������1���ֱ���x=0��y=0���ɵ�A��B��C�������꣬���ô���ϵ������ֱ��AC�Ľ���ʽΪy=kx+b��ת��Ϊ�ⷽ���鼴�ɣ�
��2����ͼ1�У���P��m��m2+2m-3���������⣬��PR���ʱ����ACP���������ı���APCO����������ΪS�ı���APCO=S��AOP+S��POC-S��AOC=![]() ��3����-m2-2m+3��+
��3����-m2-2m+3��+![]() ��3����-m��-
��3����-m��-![]() ��3��3=-
��3��3=-![]() m2-
m2-![]() m=-
m=-![]() ��m+
��m+![]() ��2+
��2+![]() �����Ե�m=-
�����Ե�m=-![]() ʱ���ı���APCO��������PR����ɵ�P��-
ʱ���ı���APCO��������PR����ɵ�P��-![]() ��-
��-![]() ��������P��BE����ƽ��
��������P��BE����ƽ��![]() ����λ�õ�G��-
����λ�õ�G��-![]() ��-
��-![]() ��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С����취�����M�����꼴�ɽ�����⣮
��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С����취�����M�����꼴�ɽ�����⣮
��3���������������ۼ��ɢ���ͼ2�У���FD1��ADʱ���ص�������Rt��FKQ������ͼ3�У���FQ��ADʱ���ص�������Rt��FQD1������ͼ4�У���QD1��ACʱ���ص�������Rt��QMF���ֱ����AQ���ɣ�
�����������1������������y=x2+2x��3����y=0����x2+2x��3=0�����x=��3��1��
��A����3��0����B��1��0����
��x=0����y=��3��
��C��0����3����
��������y=x2+2x��3=��x+1��2��4��
�ඥ��D����Ϊ����1����4����
��ֱ��AC�Ľ���ʽΪy=kx+b������![]() �����
�����![]() ��
��
��ֱ��AC�Ľ���ʽΪy=��x��3����D���꣨��1����4����
��2����ͼ1�У���P��m��m2+2m��3����
�����⣬��PR���ʱ����ACP���������ı���APCO��������
��S�ı���APCO=S��AOP+S��POC��S��AOC=![]() ��3����-m2-2m+3��+
��3����-m2-2m+3��+![]() ��3����-m��-
��3����-m��-![]() ��3��3=-
��3��3=-![]() m2-
m2-![]() m=-
m=-![]() ��m+
��m+![]() ��2+
��2+![]() ��
��
�൱m=��![]() ʱ���ı���APCO��������PR���
ʱ���ı���APCO��������PR���
��P����![]() ����
����![]() ����
����
����P��BE����ƽ��![]() ����λ�õ�G����
����λ�õ�G����![]() ����
����![]() ��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С��
��������A����ֱ��BE�ĶԳƵ�K������GK��BE��M����ʱ�ı���APNM�����С��
��ֱ��BE�Ľ���ʽΪy=��![]() x+
x+![]() ��ֱ��AK�Ľ���ʽΪy=2x+6��
��ֱ��AK�Ľ���ʽΪy=2x+6��
�� ���
���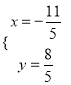 ��
��
��J����![]() ��
�� ![]() ����
����
��AJ=JK��
��k����![]() ��
�� ![]() ����
����
��ֱ��KG�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��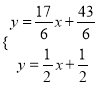 ���
���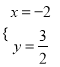 ��
��
��M����2�� ![]() ��������M����ƽ��1����λ������ƽ��2����λ�õ�N��
��������M����ƽ��1����λ������ƽ��2����λ�õ�N��
��N��0�� ![]() ����
����
��3�����ڣ�
����ͼ2�У���FD1��ADʱ���ص�������Rt��FKQ����QM��DF��M��
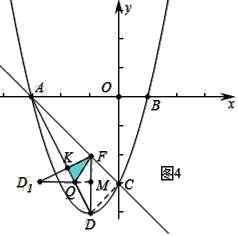
�������֪F����1����2����DF=2��AF=2![]() ��AC=3
��AC=3![]() ��AD=2
��AD=2![]()
�ɡ�AKF�ס�ACD����![]() ��
��
��![]()
��FK=![]() ��AK=
��AK=![]() ��
��
��DK=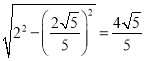 ����QK=QM=x��
����QK=QM=x��
��Rt��QMD��x2+��2��![]() ��2=��
��2=��![]() ��x��2��
��x��2��
��x=1��![]() ��
��
��AQ=AK+KQ=1+![]()
����ͼ3�У���FQ��ADʱ���ص�������Rt��FQD1����ʱAQ=![]() ��
��
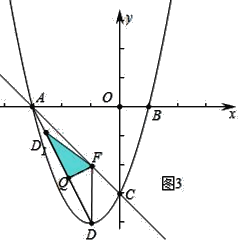
����ͼ4�У���QD1��ACʱ���ص�������Rt��QMF��
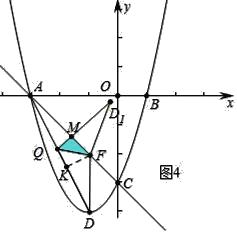
��QM=QK=x����Rt��AQM��x2+��2![]() ��
��![]() ��2=��
��2=��![]() ��x��2��
��x��2��
��x=![]()
��AQ=AK��QK=![]() ����
����![]() ��=
��=![]() ��
��
��������������D1FQ���AFQ�ص����ֵ�ͼ����ֱ��������ʱ��AQ�ij�Ϊ1+![]() ��
��![]() ��
��![]() ��
��

 ��ҵ����ϵ�д�
��ҵ����ϵ�д�����Ŀ��ij��˾��Ƹ�˲ţ���ӦƸ�߷ֱ�����Ķ�������רҵ֪ʶ����������������ԣ�����������Ե÷ְ�3��5��2�ı���ȷ��ÿ�˵����ճɼ��������Ӽ�����ѡ����¼ȡһ�ˣ���֪���˵ĸ�����Ե÷����±�(��λ����)
�Ķ� | רҵ | ���� | |
�� | 93 | 86 | 73 |
�� | 95 | 81 | 79 |
����ͨ����صļ���˵��˭����¼�ã�
�������ѡ�߽���ӦƸ��Щ�����Ľ��飮




