题目内容
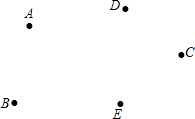 如图,同一平面内有五个点A,B,C,D,E,位置如图所示,按下列要求解答:
如图,同一平面内有五个点A,B,C,D,E,位置如图所示,按下列要求解答:(1)画直线AB;
(2)连接DA并延长DA至点M,使AM=2DA;
(3)在平面内是否存在一点P,使PA+PE+PC+PD最小?若存在,在图中画出点P,并简要说明理由;若不存在,直接回答不存在.
考点:直线、射线、线段,线段的性质:两点之间线段最短
专题:
分析:(1)连接AB,并向两方无限延长;
(2)连接DA,并沿DA方向延长,使AM=2AD;
(3)根据两点之间线断最短可得点P在DE、AC的交点处.
(2)连接DA,并沿DA方向延长,使AM=2AD;
(3)根据两点之间线断最短可得点P在DE、AC的交点处.
解答:解:(1)如图所示 ;
;
(2)如图所示;
(3)连接DE、AC,相交于点P,根据两点之间,线段最短.
 ;
;(2)如图所示;
(3)连接DE、AC,相交于点P,根据两点之间,线段最短.
点评:此题主要考查了直线、射线和线段,关键是掌握三线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )| A、60° | B、50° |
| C、45° | D、30° |
 如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
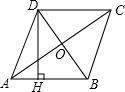 如图,菱形ABCD的对角线相交于点O,AC=16cm,周长为40cm,求菱形的高DH的长.
如图,菱形ABCD的对角线相交于点O,AC=16cm,周长为40cm,求菱形的高DH的长. 点a,b在数轴上的位置如图,则a+b
点a,b在数轴上的位置如图,则a+b 如图,正比例函数y=k1x与反比例函数y=
如图,正比例函数y=k1x与反比例函数y=