题目内容
观察下列各式:
1×
=
,1-
=
;
×
=
,
-
=
;
=
;
-
=
;
…
(1)请推测
等于什么?(其中n为正整数)
(2)根据推测的结果,计算:
+
+
+…+
.
1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3×4 |
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
…
(1)请推测
| 1 |
| n×(n+1) |
(2)根据推测的结果,计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2012×2013 |
考点:规律型:数字的变化类
专题:
分析:(1)分子是1,分母是连续自然数的乘积等于分子是1,以这两个自然数为分母的分数的差,由此直接写出答案即可;
(2)利用规律拆项,进一步相互抵消得出答案即可.
(2)利用规律拆项,进一步相互抵消得出答案即可.
解答:解:(1)
=
-
.
(2)
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2012×2013 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2012 |
| 1 |
| 2013 |
=1-
| 1 |
| 2013 |
=
| 2012 |
| 2013 |
点评:此题考查数字的变化规律,找出规律,利用规律解决问题.

练习册系列答案
相关题目
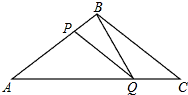 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿着AB以每秒4cm的速度向点B运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向点A运动.设运动时间为x.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿着AB以每秒4cm的速度向点B运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向点A运动.设运动时间为x.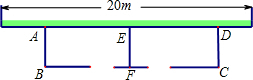 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米. 如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.
如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.