题目内容
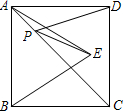 如图,正方形ABCD的面积为36cm2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为
如图,正方形ABCD的面积为36cm2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为考点:轴对称-最短路线问题,正方形的性质
专题:
分析:根据正方形的面积求出边长,根据正方形的性质,点B、D关于AC对称,再根据轴对称确定最短路线问题,BE与AC的交点即为所求的使PD+PE的和最小时的点P的位置,然后根据PD+PE=BE计算即可得解.
解答:解:∵正方形ABCD的面积为36cm2,
∴边长AB=6cm,
∵△ABE是等边三角形,
∴BE=AB=6cm,
由正方形的对称性,点B、D关于AC对称,
∴BE与AC的交点即为所求的使PD+PE的和最小时的点P的位置,
∴PD+PE的和的最小值=BE=6cm.
故答案为:6cm.
∴边长AB=6cm,
∵△ABE是等边三角形,
∴BE=AB=6cm,
由正方形的对称性,点B、D关于AC对称,
∴BE与AC的交点即为所求的使PD+PE的和最小时的点P的位置,
∴PD+PE的和的最小值=BE=6cm.
故答案为:6cm.
点评:本题考查了轴对称确定最短路线问题,正方形的对称性,熟记性质以及最短路线的确定方法确定出PD+PE的和的最小值=BE是解题的关键.

练习册系列答案
相关题目
一次函数y=kx+b的图象经过A(-1,1),B(4,0)两点,若点M(2,y1)和点N(3,y2)恰好也是该函数图象上的两点,则y1,y2的关系是( )
| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、无法确定 |
 如图,AB∥CD,∠A=73°,则∠1的度数为( )
如图,AB∥CD,∠A=73°,则∠1的度数为( )| A、127° | B、107° |
| C、110° | D、117° |
已知点A(2m-4,4-m)在第四象限,则m的取值范围是( )
| A、m>4 | B、m>2 |
| C、2<m<4 | D、-4<m<2 |
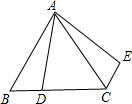 如图,在等边三角形ABC中,AB=9,D是BC边上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为
如图,在等边三角形ABC中,AB=9,D是BC边上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为