题目内容
14.已知x-5y=0,求$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}•\frac{x+3y}{x+y}$的值.分析 首先将分子与分母因式分解,进而化简求出即可.
解答 解:$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}•\frac{x+3y}{x+y}$
=$\frac{(x+y)(x-y)}{(x-y)^{2}}$×$\frac{x+3y}{x+y}$
=$\frac{x+3y}{x-y}$,
∵x-5y=0,∴x=5y,
则原式=$\frac{5y+3y}{3y-y}$=4.
点评 此题主要考查了分式的化简求值,正确因式分解得出是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
6.已知反比例函数y=$\frac{10}{x}$,当1<x<2时,y的取值范围是( )
| A. | 1<y<2 | B. | 5<y<10 | C. | 0<y<5 | D. | y>10 |
4.某中学2012年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2014年投资18.59万元.则该学校为新增电脑投资的年平均增长率为( )
| A. | 18% | B. | 15% | C. | 28% | D. | 30% |
 如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是-1,则顶点A的坐标是(2,1).
如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是-1,则顶点A的坐标是(2,1).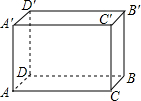 如图,已知长方体的长10cm、宽为8cm、高为6cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,则最短的路程是2$\sqrt{74}$cm.
如图,已知长方体的长10cm、宽为8cm、高为6cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,则最短的路程是2$\sqrt{74}$cm.