题目内容
3.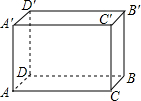 如图,已知长方体的长10cm、宽为8cm、高为6cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,则最短的路程是2$\sqrt{74}$cm.
如图,已知长方体的长10cm、宽为8cm、高为6cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,则最短的路程是2$\sqrt{74}$cm.
分析 根据题意画出长方体的侧面展开图,根据勾股定理求解即可.
解答  解:如图1所示,
解:如图1所示,
AB′=$\sqrt{(10+8)^{2}+{6}^{2}}$=6$\sqrt{10}$(cm);
如图2所示,
AB′=$\sqrt{{(6+8)}^{2}+{10}^{2}}$=2$\sqrt{74}$(cm).
∵6$\sqrt{10}$>2$\sqrt{74}$,
∴从A点爬到B′点的最短距离是2$\sqrt{74}$cm.
故答案为:2$\sqrt{74}$.
点评 本题考查的是平面展开-最短路径问题,根据题意画出长方体的侧面展开图示是解答此题的关键.

练习册系列答案
相关题目
11.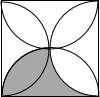 如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
 如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
8. 已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为( )
已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为( )
 已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为( )
已知在正方形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,若AD=8cm,则OE的长为( )| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |
12.函数y=$\frac{k}{x}$的图象经过点(2,1),则k的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
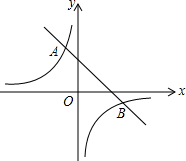 如图,一次函数y=-x+2的图象与反比例函数y=(k为常数且k≠0)的图象交于点A(-1,m).
如图,一次函数y=-x+2的图象与反比例函数y=(k为常数且k≠0)的图象交于点A(-1,m).