题目内容
5. 如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为32.
如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为32.
分析 根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
解答 解:∵△A1B1A2是等边三角形,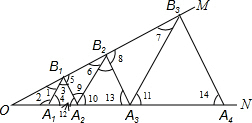
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=2,
∴A2B1=2,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A6B6=32B1A2=32.
故答案是:32.
点评 此题主要考查了等边三角形的性质以及等腰三角形的性质,根据已知得出A3B3=4B1A2,A4B4=8B1A2,A5B5=16B1A2进而发现规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列说法:①-$\sqrt{17}$是17的一个平方根;②$\frac{1}{27}$的立方根是$±\frac{1}{3}$;③0.1的算术平方根是0.01;④实数和数轴上的点一一对应.其中,正确的有( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
17.若等腰三角形一边长为5,另一边长为6,则这个三角形的周长是( )
| A. | 16 | B. | 17 | C. | 16或17 | D. | 15 |
14. 如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,若S△DEF=5,则S△BCF等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,若S△DEF=5,则S△BCF等于( )
 如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,若S△DEF=5,则S△BCF等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,若S△DEF=5,则S△BCF等于( )| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
15.下列选项中一元二次方程的是( )
| A. | x=2y-3 | B. | 2(x+1)=3 | C. | 2x2+x-4 | D. | 5x2+3x-4=0 |