题目内容
 直线AD上有A、B、C、D四个站,要建1个加油站M,使得加油站M到各个站之间路程和最小,问加油站建在何处.
直线AD上有A、B、C、D四个站,要建1个加油站M,使得加油站M到各个站之间路程和最小,问加油站建在何处.考点:比较线段的长短
专题:
分析:分别讨论超市M的位置,①A、B之间;②B、C之间;③C、D之间,然后即可确定位置.
解答:解:①若M在A、B(包含A,不包含B)之间,如图①所示:

则总路程为:AM+BM+CM+DM=AD+BC+2BM;
②若M在B、C(包含B,包含C)之间,如图②所示:

则总路程为:AM+BM+CM+DM=AD+BC;
③若M在C、D(不包含C,包含D)之间,如图③所示:

则总路程为:AM+BM+CM+DM=AD+BC+2CM;
综上可得大型超市M修在B、C处或B、C之间总路程最小,

则总路程为:AM+BM+CM+DM=AD+BC+2BM;
②若M在B、C(包含B,包含C)之间,如图②所示:

则总路程为:AM+BM+CM+DM=AD+BC;
③若M在C、D(不包含C,包含D)之间,如图③所示:

则总路程为:AM+BM+CM+DM=AD+BC+2CM;
综上可得大型超市M修在B、C处或B、C之间总路程最小,
点评:本题考查了比较两条线段长短,关键是分类讨论,要使总路程和最短,就要保证重复走的路程最小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB是⊙O直径,∠AOC=140°,则∠D=( )
如图,AB是⊙O直径,∠AOC=140°,则∠D=( )| A、55° | B、25° |
| C、20° | D、15° |
 已知:如图,CD⊥AB,EF⊥AB,垂足分别为D、F,CD=EF,AD=BF.求证:∠A=∠B.
已知:如图,CD⊥AB,EF⊥AB,垂足分别为D、F,CD=EF,AD=BF.求证:∠A=∠B.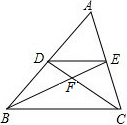 如图,在△ABC中,D为AB中点,E为AC上一点,且
如图,在△ABC中,D为AB中点,E为AC上一点,且 在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.
在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF. 如图:在Rt△ABC中,∠ACB=90°,P为AB上一点,Q为BC上一点,且PQ⊥AB,若△BPQ的面积等于四边形APQC的面积的
如图:在Rt△ABC中,∠ACB=90°,P为AB上一点,Q为BC上一点,且PQ⊥AB,若△BPQ的面积等于四边形APQC的面积的 如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若
如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若