题目内容
用换元法解方程
解：设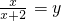
，则原方程可化得y2-5y+6=0，
解这个方程得y1=2，y2=3．
当y=2时，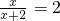
，去分母得x=2x+4，∴x1=-4
当y=3时，
，去分母得x=3x+6，∴x2=-3
经检验，x1=-4，x2=-3都是原方程的解．
∴原方程的解是x1=-4，x2=-3．
分析：先设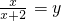，则原方程可化得y2-5y+6=0，求得y的值，代入求出x的值即可．
点评：本题考查了用换元法解方程，解题关键是能准确的找出可用替换的代数式
，再用字母y代替解方程．
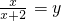，则原方程可化得y2-5y+6=0，解这个方程得y1=2，y2=3．
当y=2时，
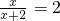，去分母得x=2x+4，∴x1=-4当y=3时，
，去分母得x=3x+6，∴x2=-3经检验，x1=-4，x2=-3都是原方程的解．
∴原方程的解是x1=-4，x2=-3．
分析：先设
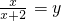，则原方程可化得y2-5y+6=0，求得y的值，代入求出x的值即可．点评：本题考查了用换元法解方程，解题关键是能准确的找出可用替换的代数式
，再用字母y代替解方程． 
练习册系列答案
活力课时同步练习册系列答案
相关题目
用换元法解方程(x+
)2-(x+
)=2，若设a=x+
，则方程可化为（ ）
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| A、a2+a+2=0 |
| B、a2-a+2=0 |
| C、a2-a-2=0 |
| D、a2+a-2=0 |
用换元法解方程（x-
）2-3x+
+2=0时，如果设x-
=y，那么原方程可转化（ ）
| 1 |
| x |
| 3 |
| x |
| 1 |
| x |
| A、y2+3y+2=0 |
| B、y2-3y-2=0 |
| C、y2+3y-2=0 |
| D、y2-3y+2=0 |