题目内容
13.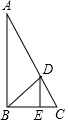 如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D、E为垂足,下列结论正确的是( )
如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D、E为垂足,下列结论正确的是( )| A. | AC=2AB | B. | AC=8EC | C. | CE=$\frac{1}{2}$BD | D. | BC=2BD |
分析 根据30°角所对的直角边等于斜边的一半得出BC=$\frac{1}{2}$AC,BD=$\frac{1}{2}$AB,CE=$\frac{1}{2}$CD,CD=$\frac{1}{2}$BC,从而得出CE=$\frac{1}{2}$CD=$\frac{1}{4}$BC=$\frac{1}{8}$AC,进而求解即可.
解答 解:∵在△ABC中,∠ABC=90°,∠A=30°,
∴BC=$\frac{1}{2}$AC,故A选项错误.
∵BD⊥AC,DE⊥BC,D、E为垂足,
∴BD=$\frac{1}{2}$AB,CE=$\frac{1}{2}$CD,故C、D选项错误;
∵∠CBD=∠A=90°-∠ABD,
∴CD=$\frac{1}{2}$BC,
∴CE=$\frac{1}{2}$CD=$\frac{1}{4}$BC=$\frac{1}{8}$AC,
∴AC=8CE,故B选项正确.
故选B.
点评 本题主要考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了余角的性质以及三角形的高的定义.

练习册系列答案
相关题目
3.某商品现在的售价为每件30元,每天可卖出40件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?设每件商品降价x元,每天的销售额为y元.
(1)分析:根据问题中的数量关系,用含x的式子填表:
(2)由以上分析,用含x的式子表示y,并求出问题的解.
(1)分析:根据问题中的数量关系,用含x的式子填表:
| 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 | |
| 每件售价(元) | 30 | 29 | 28 | … | 30-x |
| 每天销量(件) | 40 | 42 | 44 | … | 40+2x |
1.把根号外的因式化到根号内:-a$\sqrt{-a}$=( )
| A. | $\sqrt{-{a}^{2}}$ | B. | $\sqrt{-{a}^{3}}$ | C. | -$\sqrt{-{a}^{3}}$ | D. | $\sqrt{{a}^{3}}$ |
8.在-0.25、+2.3、0、-$\frac{3}{2}$这四个数中,最小的数是( )
| A. | -0.25 | B. | +2.3 | C. | 0 | D. | -$\frac{3}{2}$ |
5.二次函数y=x2+bx+c中,若c-b=0,则它的图象一定过点( )
| A. | (1,-1) | B. | (-1,1) | C. | (1,0) | D. | (-1,0) |
2.下列变形错误的是( )
| A. | 若-$\frac{1}{2}$x=6,则x=-12 | B. | 若3x=x+1,则2x=1 | ||
| C. | 若x2=y2,则x=y | D. | 若x=y,则x2=y2 |
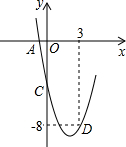 二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).
二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).