题目内容
若当x=-2时代数式ax3+bx-1的值是2，那么当x=2时该代数式的值是 ．
考点：代数式求值
专题：
分析：因为x=2与x=-2互为相反数，且代数式中x的幂指数都为奇数，所以当x=2时，代数式（ax3+bx）的值与x=-2时的值互为相反数
解答：解：∵x=2与x=-2互为相反数，且代数式中x的幂指数都为奇数，
当x=-2时，ax3+bx-1=2，
∴ax3+bx=1+2=3，
∴当x=2时，原式=-（ax3+bx）-1=-3-1=-4．
故答案为：-4
当x=-2时，ax3+bx-1=2，
∴ax3+bx=1+2=3，
∴当x=2时，原式=-（ax3+bx）-1=-3-1=-4．
故答案为：-4
点评：主要考查相反数的概念及性质，要注意是代数式（ax3+bx）的值互为相反数，而不是整个代数式，是易错题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
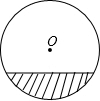如图是一条水平铺设的直径为2米的通水管道横截面，当管道中水深为0.4米时，水面宽为
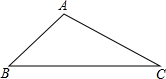作图题：（要求保留作图痕迹，不写作法）
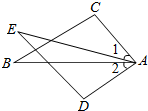如图，已知∠1=∠2，AC=AD，添加一个条件使△ABC≌△AED，你添加的条件是
实数a，b在数轴上对应点的位置如图所示，则ab如果|a+2|与（b-1）2互为相反数，那么代数式（a+b）2011的值是（ ）
| A、1 | B、-1 | C、±1 | D、2008 |