题目内容
3. 如图,四边形ABCD是菱形,点E、F、G、H是AD、AB、BC、CD的中点.
如图,四边形ABCD是菱形,点E、F、G、H是AD、AB、BC、CD的中点.(1)求证:四边形EFGH是矩形;
(2)若菱形ABCD的面积是50,求四边形EFGH的面积.
分析 (1)根据三角形的中位线定理,即可证明四边形EFGH的两组对边分别平行,即为平行四边形,然后根据平行线证明有一个角是直角,即可依据矩形的定义得出结论;
(2)根据菱形的性质可得,菱形的面积=$\frac{1}{2}$×AC×BD,由三角形中位线定理可得,EH=$\frac{1}{2}$AC,EF=$\frac{1}{2}$BD,根据四边形EFGH是矩形,可求得矩形的面积.
解答  (1)证明:∵F、E是AB和AD的中点,即EF是△ABD的中位线,
(1)证明:∵F、E是AB和AD的中点,即EF是△ABD的中位线,
∴BD∥EF,
同理可得:EH∥AC,HG∥BD,FG∥AC,
∴EH∥FG,且EF∥HG.
∴四边形EFGH是平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴EH⊥HG,
即∠EHG=90°,
∴平行四边形EFGH是矩形;
(2)解:∵菱形ABCD的面积是50,
∴$\frac{1}{2}$×AC×BD=50,
又∵F、E、H是AB、AD、CD的中点,
∴EF是△ABD的中位线,EH是△ACD的中位线,
∴EH=$\frac{1}{2}$AC,EF=$\frac{1}{2}$BD,
∴矩形EFGH的面积=EF•EH=$\frac{1}{2}$AC×$\frac{1}{2}$BD=$\frac{1}{2}$×50=25.
点评 本题以中点四边形为背景,主要考查了三角形的中位线定理以及矩形的判定方法,正确理解矩形的判定方法是关键.解答该时注意:菱形面积=$\frac{1}{2}$ab(其中a、b是两条对角线的长度).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.化简
(1)-7mn+mn+5nm
(2)(2-m2+4m)-(5m2-m-1)
(3)(-3a2-2a)-[a2-2(5a-4a2+1)-3a]
(4)5x2-(3y2+7xy)+2(2y2-5x2)
(1)-7mn+mn+5nm
(2)(2-m2+4m)-(5m2-m-1)
(3)(-3a2-2a)-[a2-2(5a-4a2+1)-3a]
(4)5x2-(3y2+7xy)+2(2y2-5x2)
8.下列各数中,最小的数是( )
| A. | -4 | B. | -2 | C. | 1 | D. | $\frac{1}{2}$ |

 如图,在正方形ABCD中,分别以AD、BC为边作Rt△ADE和Rt△BFC,延长DE、FB交于点P,延长FC、AE交于点Q,连接AP、QB,延长QB交PD于点N,交AP于点M,若PD=$\sqrt{5}$AM,PM=2BN,则tan∠DAQ的值为$\frac{8\sqrt{5}}{15}$.
如图,在正方形ABCD中,分别以AD、BC为边作Rt△ADE和Rt△BFC,延长DE、FB交于点P,延长FC、AE交于点Q,连接AP、QB,延长QB交PD于点N,交AP于点M,若PD=$\sqrt{5}$AM,PM=2BN,则tan∠DAQ的值为$\frac{8\sqrt{5}}{15}$. 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{n}$AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{n}$AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.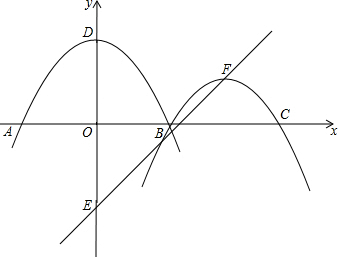 如图:二次函数y=ax2+c(a<0,c>0)的图象C1交
如图:二次函数y=ax2+c(a<0,c>0)的图象C1交