题目内容
 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,∠ABC=45°,∠BAC=75°,CD=5cm,则BF=
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,∠ABC=45°,∠BAC=75°,CD=5cm,则BF=考点:含30度角的直角三角形
专题:
分析:由条件可证明△BDF≌△ADC,再结合直角三角形的性质可得BF=AC=2CD,可得出答案.
解答:解:∵AD⊥BC,∠ABC=45°,
∴BD=AD,∠BDF=∠ADC=90°,
∵BE⊥AC,
∴∠FBD+∠C=∠CAD+∠C=90°,
∴∠FBD=∠CAD,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA),
∴BF=AC,
∵∠BAC=75°,∠BAD=45°,
∴∠DAC=30°,
∴AC=2CD=10cm,
∴BF=10cm,
故答案为:10cm.
∴BD=AD,∠BDF=∠ADC=90°,
∵BE⊥AC,
∴∠FBD+∠C=∠CAD+∠C=90°,
∴∠FBD=∠CAD,
在△BDF和△ADC中,
|
∴△BDF≌△ADC(ASA),
∴BF=AC,
∵∠BAC=75°,∠BAD=45°,
∴∠DAC=30°,
∴AC=2CD=10cm,
∴BF=10cm,
故答案为:10cm.
点评:本题主要考查全等三角形的判定和性质及直角三角形的性质,证明△BDF≌△ADC得到BF=AC是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
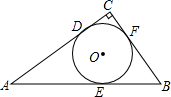 如图,⊙O是Rt△ABC的内切圆,∠C=90°,若AC=12cm,BC=9cm,则⊙O的半径( )
如图,⊙O是Rt△ABC的内切圆,∠C=90°,若AC=12cm,BC=9cm,则⊙O的半径( )| A、3cm | B、6cm |
| C、9cm | D、15cm |
在-1
,1.2,-2,0,-(-2),(-1)2015中,负数的个数有( )
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
若直线y=-x向上平移3个单位后得到直线y=kx+1,则k的值为( )
| A、-1 | B、3 | C、1 | D、-3 |
 在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.已知格点△ABC.
在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.已知格点△ABC. 如图所示,是小军同学在平整的桌面上用七个大小相同的小正方体搭成的几何体,请你画出这个几何体的三视图.
如图所示,是小军同学在平整的桌面上用七个大小相同的小正方体搭成的几何体,请你画出这个几何体的三视图.