题目内容
12. 如图,在梯形ABCD中,AD∥BC,∠B=45°,AD=8,AB=$10\sqrt{2}$,CD=26,求BC的长.
如图,在梯形ABCD中,AD∥BC,∠B=45°,AD=8,AB=$10\sqrt{2}$,CD=26,求BC的长.
分析 作AE⊥BC,DF⊥BC,垂足分别为E、F,由此可得出四边形AEFD是矩形,在Rt△ABE中利用勾股定理可求出AE的长,在Rt△DFC中利用勾股定理可求出FC的长,再根据线段之间的关系即可得出BC的长.
解答 解:作AE⊥BC,DF⊥BC,垂足分别为E、F,如图所示.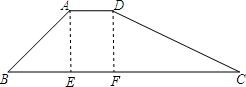
∵AE⊥BC,DF⊥BC,
∴∠AEF=∠DFE=90°,AE∥DF.
∵AD∥BC,
∴四边形AEFD是矩形,
∴AE=DF,AD=EF=8.
在Rt△ABE中,由∠B=45°,得AE=BE
∴$AB=\sqrt{A{E^2}+B{E^2}}=\sqrt{2}AE=10\sqrt{2}$,
∴AE=BE=10,
∴DF=10.
在Rt△DFC中,由DF=10,CD=26,
∴FC=$\sqrt{C{D}^{2}-D{F}^{2}}$=24,
∴BC=BE+EF+FC=42.
点评 本题考查了梯形的性质及直角三角形的性质,属于基础题,关键将掌握的知识结合,做题时融会贯通.

练习册系列答案
相关题目
3.下列调查中,适合用全面调查的是( )
| A. | 调査某批次汽车的抗撞击能力 | |
| B. | 鞋厂检测生产鞋底能承受的弯折次数 | |
| C. | 了解某班学生的身髙情况 | |
| D. | 调査市场上某种产品的色素含量是否符备国家标准 |
2.反比例函数y=-$\frac{1}{x}$的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( )
| A. | y1<y2<0 | B. | y1<0<y2 | C. | y1>y2>0 | D. | y1>0>y2 |


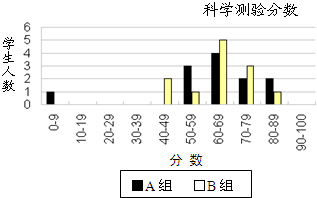 如图是两组学生参加科学测验的结果,这两组学生分别称为A组和B组.A组的平均分数是62.0分,B组的平均分数是64.5分.当学生得分为50分或以上时他们便通过这个测验.由图,老师认为B组学生比A组学生的表现好.但A组学生不同意老师的看法.他们说服老师B组学生并不一定好.依据上图,写出一个A组学生可能使用的数学论点是合格总人数A组多于B组.
如图是两组学生参加科学测验的结果,这两组学生分别称为A组和B组.A组的平均分数是62.0分,B组的平均分数是64.5分.当学生得分为50分或以上时他们便通过这个测验.由图,老师认为B组学生比A组学生的表现好.但A组学生不同意老师的看法.他们说服老师B组学生并不一定好.依据上图,写出一个A组学生可能使用的数学论点是合格总人数A组多于B组.