题目内容
17.如图1,在锐角△ABC中,AD是BC边上的高,BC=6,AD=4,动点P沿线段AD从点A向点D运动,过点P作EF∥BC,EF交AB于E.交AC于F,以EF为边向下作正方形EFGH.(1)设AP长为x,利用相似三角形的性质.可用含x的代数式表示正方形的边长为EF=$\frac{3}{2}$x;如图2,当x=$\frac{8}{5}$时,GH恰好落在边BC上,此时EF长为$\frac{12}{5}$;
(2)如图3,当GH在△ABC外部,且正方形EFGH与△ABC公共部分的面积为6时,求点P的位置(即求AP的值)
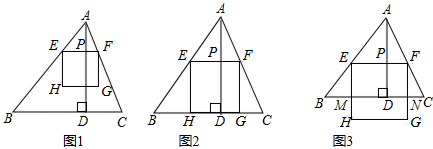
分析 (1)由EF∥BC,推出△AEF∽△ABC,根据相似三角形的性质得到$\frac{AP}{AD}=\frac{EF}{BC}$,求出EF=$\frac{3}{2}$x,当GH恰好落在边BC上时,得到AP+PD=AP+EF=AD,列方程x+$\frac{3}{2}$x=4,解得:x=$\frac{8}{5}$,即可得到结论;
(2)设EH交BC于G,则EM=PD=AD-AP=4-x,根据EF•EM=6,于是得到方程$\frac{3}{2}$x•(4-x)=6,即可得到AP=2,当AP=2时,AP<AD,点P在△ABC的内部,满足题意.
解答 解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AP}{AD}=\frac{EF}{BC}$,
∴EF=$\frac{3}{2}$x,
当GH恰好落在边BC上时,
AP+PD=AP+EF=AD,
∴x+$\frac{3}{2}$x=4,
解得:x=$\frac{8}{5}$,
∴EF=$\frac{3}{2}$x=$\frac{12}{5}$;
故答案为:$\frac{3}{2}$x,$\frac{8}{5}$,$\frac{12}{5}$;
(2)设EH交BC于G,则EM=PD=AD-AP=4-x,
∵正方形EFGH与△ABC公共部分的面积为6,
∴EF•EM=6,
∴$\frac{3}{2}$x•(4-x)=6,
解得:x=2,
即AP=2,
当AP=2时,AP<AD,点P在△ABC的内部,满足题意.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列说法中,不正确的是( )
| A. | 10的立方根是$\root{3}{10}$ | B. | $\frac{4}{9}$的平方根是$\frac{2}{3}$ | ||
| C. | -2是4的一个平方根 | D. | 0.01的算术平方根是0.1 |
9.下列说法正确的是( )
| A. | 无限小数都是无理数 | B. | (-4)2的平方根是4 | ||
| C. | 无理数的相反数还是无理数 | D. | 无理数的倒数不一定是无理数 |
6.规定一种新的运算x?y=x-y2,则-2?3等于( )
| A. | -11 | B. | -7 | C. | -8 | D. | 25 |
 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.