题目内容
8.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①f(a,b)=(-a,b).如:f(1,3)=(-1,3);
②g(a,b)=(b,a).如:g(1,3)=(3,1);
③h(a,b)=(-a,-b).如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),
则f(h(5,-3))的值为(5,3);g(f(5,-3))的值为(-3,-5).
分析 首先根据h(a,b)=(-a,-b),f(a,b)=(-a,b),求出f(h(5,-3))的值为多少即可;然后根据f(a,b)=(-a,b),g(a,b)=(b,a),求出g(f(5,-3))的值为多少即可.
解答 解:f(h(5,-3))=f(-5,3)=(5,3),
g(f(5,-3))=g(-5,-3)=(-3,-5).
故答案为:(5,3)、(-3,-5).
点评 此题主要考查了点的坐标,要熟练掌握,解答此题的关键是要熟练掌握三种变换的方法.

练习册系列答案
相关题目
18.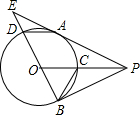 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )| A. | ①③④ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
13. 如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
 如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )| A. | $\sqrt{13}$ | B. | 6 | C. | 2$\sqrt{13}$ | D. | 10 |
17.下列各数中,最大的数是( )
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 1 |
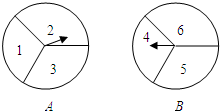 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
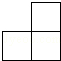
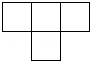
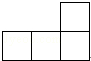
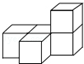 如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )
如图是由五个完全相同的小正方体组成的几何体,这个几何体的俯视图是( )