题目内容
已知x>y,试比较
+y和2x的大小.
| x2 |
| y |
考点:因式分解的应用
专题:计算题
分析:利用求差比较大小,计算
+y-2x=
,易(x-y)2>0,然后分类讨论:当y>0或y<0时,比较
+y和2x的大小.
| x2 |
| y |
| (x-y)2 |
| y |
| x2 |
| y |
解答:解:
+y-2x=
=
,
∵x>y,
∴(x-y)2>0,
当y>0时,则
>0,所以
+y>2x;
当y<0时,则
<0,所以
+y<2x.
| x2 |
| y |
| x2-2xy+y2 |
| y |
| (x-y)2 |
| y |
∵x>y,
∴(x-y)2>0,
当y>0时,则
| (x-y)2 |
| y |
| x2 |
| y |
当y<0时,则
| (x-y)2 |
| y |
| x2 |
| y |
点评:本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
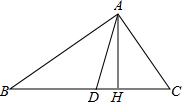 如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长.
如图,在△ABC中,∠ACB=90°,CD为∠ACB的角平分线,CH⊥AB于H,若AD=p,BD=q,求CH的长. 一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30
一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30