题目内容
1．
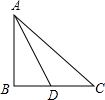如图，△ABC中，∠B=90°，AD平分∠BAC，且∠C=4∠BAD，求∠ADC的度数．
分析 由直角三角形的性质得出∠BAC+∠C=90°，再由已知条件得出2∠BAD+4∠BAD=90°，求出∠BAD=15°，由三角形的外角性质即可得出∠ADC的度数．
解答 解：∵∠B=90°，
∴∠BAC+∠C=90°，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵∠C=4∠BAD，
∴2∠BAD+4∠BAD=90°，
∴∠BAD=∠CAD=15°，
∴∠ADC=∠BAD+∠B=15°+90°=105°．
点评 本题考查了直角三角形的性质、三角形内角和定理、三角形的外角性质；熟练掌握直角三角形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
9．二次根式$\sqrt{-2x^3}$可化简为（ ）
| A． | x$\sqrt{-2x}$ | B． | -x$\sqrt{-2x}$ | C． | -$\sqrt{2x^3}$ | D． | x2$\sqrt{-\frac{2}{x}}$ |
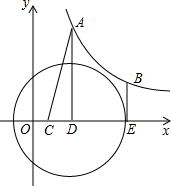如图所示：点A，B是反比例函数y=$\frac{k}{x}$（x＞0）图象上的两个动点，分别过点A、B点作AD⊥x轴于D，BE⊥x轴于E，点C是线段OD的中点．