题目内容
12.在等边△ABC中,D是BC的中点,连接AD,点E在AC上,且AE=AD,连接DE,根据题意画出示意图,并求∠CAD和∠CDE的度数.分析 根据题意画出图形,先根据等腰三角形三线合一的性质求出∠DAC的度数,再由三角形内角和定理求出∠ADE的度数,进而可得出∠CDE的度数.
解答  解:如图所示,
解:如图所示,
∵△ABC是等边三角形,D是BC的中点,
∴∠BAC=60°,AD⊥BC,
∴∠CAD=$\frac{1}{2}$∠BAC=30°,∠ADC=90°.
∵AE=AD,
∴∠ADE=$\frac{180°-30°}{2}$=75°,
∴∠CDE=90°-75°=15°.
点评 本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
3.在△ABC和△A′B′C′中,如果AB=C′A′,BC=A′B′,CA=B′C′,那么可得结论( )
| A. | △ABC≌△A′B′C′ | B. | △ABC≌△C′A′B′ | ||
| C. | △ABC≌△C′B′A′ | D. | 这两个三角形不全等 |
4.某化肥厂生产的化肥产量经过两年增长21%,则每年比上一年平均增长的百分数为( )
| A. | 10% | B. | 10.5% | C. | 11% | D. | 12% |
9.下列各式中,运算正确的是( )
| A. | 3a-2a=1 | B. | a2+a2=a4 | C. | -3ab+2ab=-ab | D. | 2x+3y=5xy |
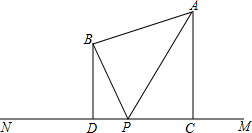 加油站A和商店B在马路MN的同一侧,A到MN的距离为5米,B到MN的距离为3米,DC=6米,行人P在马路MN上行走.P到A的距离与P到B的距离之和最小等于几米?
加油站A和商店B在马路MN的同一侧,A到MN的距离为5米,B到MN的距离为3米,DC=6米,行人P在马路MN上行走.P到A的距离与P到B的距离之和最小等于几米?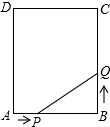 如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?
如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?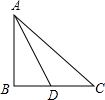 如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数.
如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数.