题目内容
16.先化简,再求值:($\frac{x}{x-1}-\frac{\sqrt{3}}{x+1}$)$÷\frac{1}{{x}^{2}-1}$,其中x=$\sqrt{3}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x(x+1)-\sqrt{3}(x-1)}{(x-1)(x+1)}$•(x+1)(x-1)
=x2+x-$\sqrt{3}$x+$\sqrt{3}$
=x2+(1-$\sqrt{3}$)x+$\sqrt{3}$,
当x=$\sqrt{3}$-1时,原式=($\sqrt{3}$-1)2+(1-$\sqrt{3}$)($\sqrt{3}$-1)+$\sqrt{3}$=8-3$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
4.某化肥厂生产的化肥产量经过两年增长21%,则每年比上一年平均增长的百分数为( )
| A. | 10% | B. | 10.5% | C. | 11% | D. | 12% |
 如图,在轮船A上测得轮船B在轮船A的南偏东50,岛C在轮船A的南偏东80°;在轮船B上测得岛C在轮船B的北偏西30°,从岛C看轮船A、B的视角∠ACB是多少度?
如图,在轮船A上测得轮船B在轮船A的南偏东50,岛C在轮船A的南偏东80°;在轮船B上测得岛C在轮船B的北偏西30°,从岛C看轮船A、B的视角∠ACB是多少度?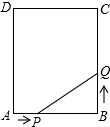 如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?
如图.矩形ABCD中,AB=6cm,BC=10cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果P、Q分别是从A、B同时出发,经过几秒,五边形APQCD的面积等于52平方厘米?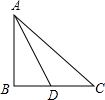 如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数.
如图,△ABC中,∠B=90°,AD平分∠BAC,且∠C=4∠BAD,求∠ADC的度数. 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.