题目内容
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是 |
| AC |
考点:圆周角定理
专题:常规题型
分析:连接AD,如图,先根据垂径定理由CD⊥AB得
=
,再根据圆周角定理得∠AGD=∠ADC,根据圆内接四边形的性质得∠FGC=∠ADC,所以∠FGC=∠AGD.
 |
| AD |
 |
| AC |
解答: 解:∠FGC与∠AGD相等.理由如下:
解:∠FGC与∠AGD相等.理由如下:
连接AD,如图,
∵CD⊥AB,
∴
=
,
∴∠AGD=∠ADC,
∵∠FGC=∠ADC,
∴∠FGC=∠AGD
 解:∠FGC与∠AGD相等.理由如下:
解:∠FGC与∠AGD相等.理由如下:连接AD,如图,
∵CD⊥AB,
∴
 |
| AD |
 |
| AC |
∴∠AGD=∠ADC,
∵∠FGC=∠ADC,
∴∠FGC=∠AGD
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和圆内接四边形的性质.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,要为一段高为5米,斜长为13米的楼梯铺上红地毯,则红地毯至少要的长度是( )
如图,要为一段高为5米,斜长为13米的楼梯铺上红地毯,则红地毯至少要的长度是( )| A、13米 | B、12米 |
| C、5米 | D、17米 |
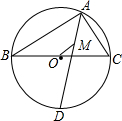 如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC,交⊙O于D,点M是△ABC的内心.
如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC,交⊙O于D,点M是△ABC的内心.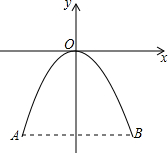 如图,一座抛物线形的拱桥,其形状可以用y=-x2来描述.
如图,一座抛物线形的拱桥,其形状可以用y=-x2来描述. 已知:∠1和∠2,作一个角,使它等于∠1-∠2.
已知:∠1和∠2,作一个角,使它等于∠1-∠2.