题目内容
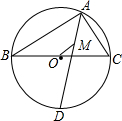 如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC,交⊙O于D,点M是△ABC的内心.
如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC,交⊙O于D,点M是△ABC的内心.(1)判断BC与DM的数量关系,并证明;
(2)若AB=8,AC=6,求AD的长.
考点:三角形的内切圆与内心
专题:计算题
分析:(1)连接DB、DC、CM,由AD平分∠BAC,根据圆周角定理得
=
,∠BDC=90°,则可判断△BCD为等腰直角三角形,所以BC=
CD,再根据三角形内心的性质得∠MCB=∠MCA,而∠DMC=∠DAC+∠MCA,∠DAC=∠BCD,易得∠DMC=∠MCD,所以DM=DC,则BC=
DM;
(2)作ME⊥AB于E,MF⊥AC于F,如图,在Rt△ABC中根据勾股定理计算出BC=10,再求出△ABC的内切圆的半径为2,根据内心的性质易得ME=MF,则可判断四边形AEMF为正方形,则AM=
ME=2
,再由(1)的结论得DM=
BC=5
,所以AD=AM+DM=7
.
 |
| BD |
 |
| CD |
| 2 |
| 2 |
(2)作ME⊥AB于E,MF⊥AC于F,如图,在Rt△ABC中根据勾股定理计算出BC=10,再求出△ABC的内切圆的半径为2,根据内心的性质易得ME=MF,则可判断四边形AEMF为正方形,则AM=
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
解答:解:(1)BC=
DM.理由如下:
连接DB、DC、CM,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴
=
,
∴BD=CD,
∵BC为直径,
∴∠BDC=90°,
∴△BCD为等腰直角三角形,
∴BC=
CD,
∵点M是△ABC的内心,
∴CM平分∠ACB,
∴∠MCB=∠MCA,
∵∠DMC=∠DAC+∠MCA,
∠DAC=∠BCD,
∴∠DMC=∠BCD+∠MCB=∠MCD,
∴DM=DC,
∴BC=
DM;
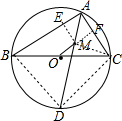 (2)作ME⊥AB于E,MF⊥AC于F,如图,
(2)作ME⊥AB于E,MF⊥AC于F,如图,
在Rt△ABC中,∵AB=8,AC=6,
∴BC=
=10,
∴△ABC的内切圆的半径=
=2,
∵点M是△ABC的内心,
∴AM平分∠BAC,
∴ME=MF,
∴四边形AEMF为正方形,
∴AM=
ME,
∴AM=2
,
而DM=
BC=5
,
∴AD=AM+DM=7
.
| 2 |
连接DB、DC、CM,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
∴BD=CD,
∵BC为直径,
∴∠BDC=90°,
∴△BCD为等腰直角三角形,
∴BC=
| 2 |
∵点M是△ABC的内心,
∴CM平分∠ACB,
∴∠MCB=∠MCA,
∵∠DMC=∠DAC+∠MCA,
∠DAC=∠BCD,
∴∠DMC=∠BCD+∠MCB=∠MCD,
∴DM=DC,
∴BC=
| 2 |
 (2)作ME⊥AB于E,MF⊥AC于F,如图,
(2)作ME⊥AB于E,MF⊥AC于F,如图,在Rt△ABC中,∵AB=8,AC=6,
∴BC=
| AB2+BC2 |
∴△ABC的内切圆的半径=
| 6+8-10 |
| 2 |
∵点M是△ABC的内心,
∴AM平分∠BAC,
∴ME=MF,
∴四边形AEMF为正方形,
∴AM=
| 2 |
∴AM=2
| 2 |
而DM=
| ||
| 2 |
| 2 |
∴AD=AM+DM=7
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,三角形的内心就是三角形三个内角角平分线的交点.记住直角边为a、b,斜边为c的三角形的内切圆半径为
.也考查了圆周角定理.
| a+b-c |
| 2 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知矩形的一条对角线长8cm,则另一条对角线长的一半是( )
| A、8cm | B、4cm |
| C、6cm | D、10cm |
下列各组数中的两个数,是互为相反数的是( )
| A、-2和-|-2| |
| B、-12和(-1)2 |
| C、23和32 |
| D、(-2)3和-23 |
近似数7.8×104是精确到( )的近似数.
| A、十分位 | B、百位 | C、千位 | D、万位 |
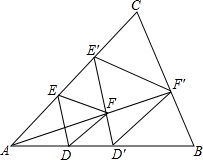 等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”,
等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”, 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是