题目内容
已知△ABC的三边长分别为6、6、8,则它的外接圆半径为 .
考点:三角形的外接圆与外心
专题:计算题
分析:如图,⊙O为△ABC的外接圆,AB=AC=6,BC=8,设它的外接圆半径为r,延长AO交BC于D,连接OB,由AB=AC得
=
,根据垂径定理的推理得AD⊥BC,BD=
BC=4,在Rt△ABD中根据勾股定理计算出AD=2
,则OD=AD-OA=2
-r,然后在Rt△OBD中利用勾股定理得到(2
-r)2+42=r2,再解一次方程即可.
 |
| AB |
 |
| AC |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
解答:解:如图, ⊙O为△ABC的外接圆,AB=AC=6,BC=8,
⊙O为△ABC的外接圆,AB=AC=6,BC=8,
设它的外接圆半径为r,
延长AO交BC于D,连接OB,
∵AB=AC,
∴
=
,
∴AD⊥BC,
∴BD=CD=
BC=4,
在Rt△ABD中,AD=
=
=2
,
∴OD=AD-OA=2
-r,
在Rt△OBD中,∵OD2+BD2=OB2,
∴(2
-r)2+42=r2,解得r=
,
即它的外接圆半径为
.
故答案为
.
 ⊙O为△ABC的外接圆,AB=AC=6,BC=8,
⊙O为△ABC的外接圆,AB=AC=6,BC=8,设它的外接圆半径为r,
延长AO交BC于D,连接OB,
∵AB=AC,
∴
 |
| AB |
 |
| AC |
∴AD⊥BC,
∴BD=CD=
| 1 |
| 2 |
在Rt△ABD中,AD=
| AB2-BD2 |
| 62-42 |
| 5 |
∴OD=AD-OA=2
| 5 |
在Rt△OBD中,∵OD2+BD2=OB2,
∴(2
| 5 |
9
| ||
| 5 |
即它的外接圆半径为
9
| ||
| 5 |
故答案为
9
| ||
| 5 |
点评:本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆;三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.会运用勾股定理计算线段的长.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
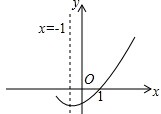 已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )
已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )| A、a+b+c=0 |
| B、b>2a |
| C、ax2+bx+c=0两根是-3和1 |
| D、a-2b+c>0 |
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E,G是 如图,已知线段a、b、m,
如图,已知线段a、b、m, 已知:△ABC
已知:△ABC