题目内容
6.设n为正整数,且n<$\sqrt{65}$<n+1,则n的值为8.分析 首先得出$\sqrt{64}$<$\sqrt{65}$$\sqrt{81}$,进而求出$\sqrt{65}$的取值范围,即可得出n的值.
解答 解:∵$\sqrt{64}$<$\sqrt{65}$<$\sqrt{81}$,
∴8<$\sqrt{65}$<9,
∵n<$\sqrt{65}$<n+1,
∴n=8,
故答案为:8.
点评 此题主要考查了估算无理数,得出$\sqrt{64}$<$\sqrt{65}$<$\sqrt{81}$是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
16.记A=$\sum_{k=1}^{2013}$$\sqrt{1+\frac{1}{{k}^{2}}+\frac{1}{(k+1)^{2}}}$,再记[A]表示不超过A的最大整数,则[A]( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 2013 |
11.下列变形正确的是( )
| A. | $\sqrt{4\frac{9}{25}}$=$\sqrt{4}$×$\sqrt{\frac{9}{25}}$=2×$\sqrt{\frac{3}{5}}$=$\frac{6}{5}$ | B. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{4{1}^{2}}$-$\sqrt{4{0}^{2}}$=41-40=1 | ||
| C. | 2$\sqrt{3}$×(-5$\sqrt{27}$)=-2×5×$\sqrt{3×27}$=-90 | D. | -3$\sqrt{2}$=$\sqrt{(-3)^{2}×2}$=$\sqrt{18}$ |
18.若n为正整数,则$\root{2n+1}{-1}$等于( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 2n+1 |
 如图,字每个小正方形的边长为1个长度单位的长方形网格中,有一个△ABC
如图,字每个小正方形的边长为1个长度单位的长方形网格中,有一个△ABC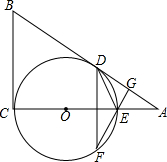 如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.
如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.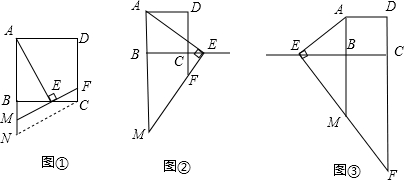
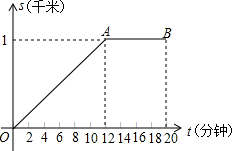 小亮早晨从家里出发匀速步行去上学,小亮的妈妈在小亮出发后10分钟,发现小亮的数学课本没带,于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮,结果与小亮同时到达学校.已知小亮在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA-AB所示.
小亮早晨从家里出发匀速步行去上学,小亮的妈妈在小亮出发后10分钟,发现小亮的数学课本没带,于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮,结果与小亮同时到达学校.已知小亮在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA-AB所示.