题目内容
8．计算下列各式（1）（-2a2bc）3+4a6b3c2；
（2）（x+3）2+（2x-3）（2x+3）-5x2；
（3）（2x-y+3）（2x+y-3）
分析 （1）根据积的乘方法则算乘方，再合并同类项即可；
（2）先算乘法，再合并同类项即可；
（3）先根据平方差公式进行计算，再根据完全平方公式进行计算即可．
解答 解：（1）（-2a2bc）3+4a6b3c2
=-8a6b3c3+4a6b3c2；
（2）（x+3）2+（2x-3）（2x+3）-5x2；
=x2+6x+9+4x2-9-5x2
=6x；
（3）（2x-y+3）（2x+y-3）
=[2x-（y-2）][2x+（y-3）]
=（2x）2-（y-3）2
=4x2-y2+6y-9．
点评 本题考查了整式的混合运算法则的应用，能熟记整式的运算法则是解此题的关键，注意：运算顺序．
练习册系列答案
相关题目
如图，马路的两边CF，DE互相平行，线段CD为人行横道，马路两侧的A，B两点分别表示车站和超市．CD与AB所在直线互相平行，且都与马路的两边垂直．马路宽20米，A，B相距62米，∠A=67°，∠B=37°．
3．
如图，图①，图②中阴影部分的面积为S1，S2，a＞b＞0，设k=$\frac{{S}_{1}}{{S}_{2}}$，则有（ ）
如图，图①，图②中阴影部分的面积为S1，S2，a＞b＞0，设k=$\frac{{S}_{1}}{{S}_{2}}$，则有（ ）| A． | 0＜k＜$\frac{1}{2}$ | B． | $\frac{1}{2}$＜k＜1 | C． | 1＜k＜2 | D． | k＞2 |
13．
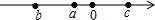已知实数a，b，c在数轴上的位置如图所示，则化简$\sqrt{{a}^{2}}$-$\sqrt{（a-b）^{2}}$-$\sqrt{（a-c）^{2}}$-$\sqrt{（b-c）^{2}}$的结果是（ ）
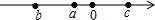已知实数a，b，c在数轴上的位置如图所示，则化简$\sqrt{{a}^{2}}$-$\sqrt{（a-b）^{2}}$-$\sqrt{（a-c）^{2}}$-$\sqrt{（b-c）^{2}}$的结果是（ ）| A． | -3a | B． | -a+2b-2c | C． | 2b | D． | a |
20．下列图形，是中心对称图形但不是轴对称图形的是（ ）
| A． | 等边三角形 | B． | 平行四边形 | C． | 圆 | D． | 正五边形 |
如图，函数y=-3x和y=kx+b的图象相交于点A（m，4），则关于x的不等式kx+b+3x＞0的解集为x＞-$\frac{4}{3}$．
18．下列各式正确的是（ ）
| A． | -8+3=5 | B． | （-2）3=6 | C． | -（a-b）=-a+b | D． | 2（a+b）=2a+b |