Question

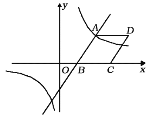
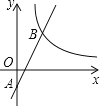
【题目】如图，在平面直角坐标系中，抛物线的顶点坐标为，与轴交于点，与轴交于点，.

（1）求二次函数的表达式；

（2）过点作平行于轴，交抛物线于点，点为抛物线上的一点（点在上方），作平行于轴交于点，当点在何位置时，四边形的面积最大？并求出最大面积.

Answer 1

【答案】（1）；（2）点的坐标为时，

【解析】

（1）根据题目已知条件，可以由顶点坐标及A点坐标先求出二次函数顶点式，进而转化为一般式即可；

（2）根据题意，先求出直线AB的解析式，再设出点P和D坐标，进而先得出四边形的面积表达式，即可求得面积最大值.

（1）∵顶点坐标为，

∴设抛物线解析式为，

∵抛物线与轴交于点，

∴，∴，

∴，

∴；

（2）当时，，∴，，

∴，，

设直线的解析式为，∵，，∴，，

∴直线的解析式为.

设，∴，

∴.

∵，∴，∴，

∵，

∴，

∵中，对称轴为，

∴当，即点的坐标为时，.