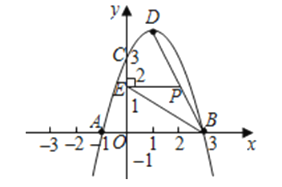Question

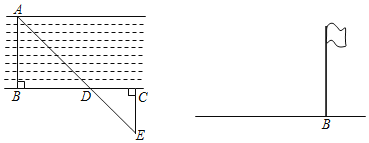
【题目】如图，是方城县潘河的某一段，现要估算河的宽度（即河两岸相对的两点A、B间的距离），可以按如下步骤操作：①先在河的对岸选定一个目标作为点A；②再在河的这一边选定点B和点C，使AB⊥BC；③再选定点E，使EC⊥BC，然后用视线确定BC和AE的交点D．

（1）用皮尺测得BC＝177米，DC＝61米，EC＝50米，求河的宽度AB；（精确到0.1米）

（2）请用所学过的知识设计一种测量旗杆高度AB的方案．

要求：①画出示意图，所测长度用a、b、c等表示，直接标注在图中线段上；

②不要求写操作步骤；③结合所测数据直接用含a、b、c等字母的式子表示出旗杆高度AB．

Answer 1

【答案】（1）两岸间的大致距离AB为95.1m；（2）详见解析．

【解析】

（1）先证明△ABD∽△ECD，然后利用相似比计算AB的长即可；

（2）在旗杆与人之间树立一个标杆，然后利用相似三角形对应边成比例求解．

解：（1）∵AB⊥BC，CE⊥BC，

∴AB∥CE，

∴△ABD∽△ECD，

∴＝，即＝，

∴AB≈（m），

答：两岸间的大致距离AB为m；

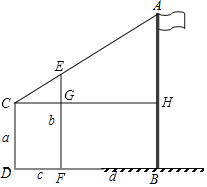
（2）如图，

①将标杆EF立在一个适当的位置；

②人CD站在一个适当的位置：通过标杆的顶部E，刚好看到旗杆的顶部A，

③测出人的身高CD=a，标杆的高度EF=b，人到标杆DF=c的距离和标杆到旗杆FB=d的距离，

④计算旗杆的高度：

过点C作CH⊥AB，交EF于G，交AB于H

易知：CG=DF=c，GF=CD=a，EG=EF－GF=b－a，GH=FB=d，CH=CG＋GH=c＋d，EF∥AB

∴△CEG∽△CAH，

∴＝，即＝，

∴AH＝

所以旗杆的高度AB＝AH+CD＝+a=．