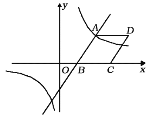
题目内容
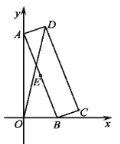
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)填空:![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,求点
在第一象限,求点![]() 的坐标;
的坐标;
【答案】(1)3,12;(2)D的坐标为![]()
【解析】
(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数
x-3,得到n的值为3;再把点A(4,3)代入反比例函数![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标.
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标.
(1)把点A(4,n)代入一次函数![]() ,可得
,可得![]() ;
;
把点A(4,3)代入反比例函数![]() ,可得
,可得![]() ,
,
解得k=12.
(2)∵一次函数![]() 与
与![]() 轴相交于点B,
轴相交于点B,
由![]() ,解得
,解得![]() ,
,
∴点B的坐标为(2,0)
如图,过点A作![]() 轴,垂足为E,
轴,垂足为E,
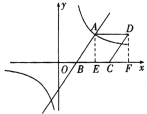
过点D作![]() 轴,垂足为F,
轴,垂足为F,
∵A(4,3),B(2,0)
∴OE=4,AE=3,OB=2,
∴ BE=OE-OB=4-2=2
在![]() 中,
中,![]() .
.
∵四边形ABCD是菱形,
∴![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() .
.
在![]() 与
与![]() 中,
中, ![]() ,
,![]() ,AB=CD,
,AB=CD,
∴![]() ,
,
∴CF=BE=2,DF=AE=3,
∴![]() .
.
∴点D的坐标为![]()

练习册系列答案
相关题目