题目内容
4.在Rt△ABC中,∠A=90°,AB=6,AC=2,则斜边上的高=$\frac{3\sqrt{10}}{5}$.分析 根据题意画出图形,根据勾股定理求出BC的长,由三角形的面积公式即可得出斜边上的高.
解答  解:如图所示,
解:如图所示,
∵在Rt△ABC中,∠A=90°,AB=6,AC=2,
∴BC=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
∴AD=$\frac{AB•AC}{BC}$=$\frac{6×2}{2\sqrt{10}}$=$\frac{3\sqrt{10}}{5}$.
故答案为:$\frac{3\sqrt{10}}{5}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
15. 如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
 如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
19.一个三角形的三个外角之比为3:4:5,则这个三角形内角之比是( )
| A. | 5:4:3 | B. | 4:3:2 | C. | 3:2:1 | D. | 5:3:1 |
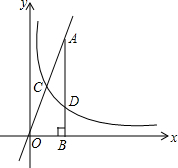 如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.