题目内容
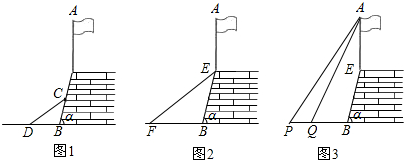
如图1,在△ABC中,∠ACB=90°,经过点B的直线l(l不与直线AB重合)与直线BC的夹角的大小等于∠ABC,分别过点C、A作直线l的垂线,垂足分别为点D、E
(1)写出线段AE、CD之间的数量关系,并加以证明;
(2)当△ABC的位置旋转到图2或图3时,设直线CE、AB交于点F,且
=
,CD=4,请你在图2和图3中任选一种情况,求此时BD的长.

(1)写出线段AE、CD之间的数量关系,并加以证明;
(2)当△ABC的位置旋转到图2或图3时,设直线CE、AB交于点F,且
| CF |
| EF |
| 5 |
| 6 |

考点:相似形综合题
专题:
分析:(1)根据△GCD∽△GAE后即可证明猜想正确.
(2)分当点F在线段AB上时和点F在线段BA的延长线上时利用△AGH∽△AEB求得线段BD的长即可.
(2)分当点F在线段AB上时和点F在线段BA的延长线上时利用△AGH∽△AEB求得线段BD的长即可.
解答:(1)线段AE、CD之间的数量关系为AE=2CD.
证明:如图1,延长AC与直线l交于点G.
依题意,可得∠1=∠2.
∵∠ACB=90°,
∴∠3=∠4.
∴BA=BG.∴CA=CG.
∵AE⊥l,CD⊥l,
∴CD∥AE.
∴△GCD∽△GAE.
,
=
=
,
∴AE=2CD.
(2)解:当点F在线段AB上时,如图2,
过点C作CG∥l交AE于点H,交AB于点G.
∴∠2=∠HCB.
∵∠1=∠2,
∴∠1=∠HCB.
∴CH=BH.
∵∠ACB=90°,
∴∠3+∠1=∠HCB+∠4=90°.
∴∠3=∠4.
∴CH=AH=BH.
∵CG∥l,
∴△FCH∽△FEB.
∴
=
=
,设CH=5x,BE=6x,则AB=10x.
∴在△AEB中,∠AEB=90°,AE=8x.
由(2)得,AE=2CD.
∵CD=4,
∴AE=8.
∴x=1.
∴AB=10,BE=6,CH=5.
∵CG∥l,
∴△AGH∽△AEB.
∴
=
=
,
∴HG=3.
∴CG=CH+HG=8.
∵CG∥l,CD∥AE,
∴四边形CDEG为平行四边形.
∴DE=CG=8.
∴BD=DE-BE=2,
当点F在线段BA的延长线上时,如图3,
同理可得CH=5,GH=3,BE=6.
∴DE=CG=CH-HG=2.
∴BD=DE+BE=8.
∴BD=2或8.
证明:如图1,延长AC与直线l交于点G.

依题意,可得∠1=∠2.
∵∠ACB=90°,
∴∠3=∠4.
∴BA=BG.∴CA=CG.
∵AE⊥l,CD⊥l,
∴CD∥AE.
∴△GCD∽△GAE.
,
| CD |
| AE |
| GC |
| GA |
| 1 |
| 2 |
∴AE=2CD.
(2)解:当点F在线段AB上时,如图2,

过点C作CG∥l交AE于点H,交AB于点G.
∴∠2=∠HCB.
∵∠1=∠2,
∴∠1=∠HCB.
∴CH=BH.
∵∠ACB=90°,
∴∠3+∠1=∠HCB+∠4=90°.
∴∠3=∠4.
∴CH=AH=BH.
∵CG∥l,
∴△FCH∽△FEB.
∴
| CF |
| EF |
| CH |
| EB |
| 5 |
| 6 |
∴在△AEB中,∠AEB=90°,AE=8x.
由(2)得,AE=2CD.
∵CD=4,
∴AE=8.
∴x=1.
∴AB=10,BE=6,CH=5.
∵CG∥l,
∴△AGH∽△AEB.
∴
| HG |
| BE |
| AH |
| AB |
| 1 |
| 2 |
∴HG=3.
∴CG=CH+HG=8.
∵CG∥l,CD∥AE,
∴四边形CDEG为平行四边形.
∴DE=CG=8.
∴BD=DE-BE=2,
当点F在线段BA的延长线上时,如图3,

同理可得CH=5,GH=3,BE=6.
∴DE=CG=CH-HG=2.
∴BD=DE+BE=8.
∴BD=2或8.
点评:本题考查了相似形综合知识的应用,题目中还涉及到了相似三角形的判定与性质及解直角三角形的知识,难度较大,此类题目应重点掌握辅助线的做法.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
四个实数-2,0,-
,1中,最大的实数是( )
| 2 |
| A、-2 | ||
| B、0 | ||
C、-
| ||
| D、1 |
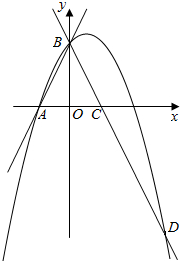 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).