题目内容
8. 如图,动点A在曲线y=$\frac{2}{x}$(x>0)上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点M,N,当NE:DM=1:2时,图中的阴影部分的面积等于$\frac{3\sqrt{2}}{2}$.
如图,动点A在曲线y=$\frac{2}{x}$(x>0)上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点M,N,当NE:DM=1:2时,图中的阴影部分的面积等于$\frac{3\sqrt{2}}{2}$.
分析 作DF⊥x轴于点F,EG⊥y轴于G,得到△NEG∽△MDF,于是得到$\frac{EG}{FM}$=$\frac{NE}{DM}$=$\frac{1}{2}$,设EG=t,则MF=2t,然后根据△ADE∽△FMD,据此即可得到关于t的方程,求得t2的值,进而求解.
解答 解:作DF⊥x轴于点F,EG⊥y轴于G,
∴△NEG∽△DMF,
∴$\frac{EG}{MF}$=$\frac{NE}{DM}$=$\frac{1}{2}$,
设EG=t,则MF=2t,
∴A(t,$\frac{2}{t}$),
∵AC=AE,AD=AB,
∴AE=t,AD=$\frac{2}{t}$,DF=$\frac{2}{t}$,MF=2t,
∵△ADE∽△FMD,
∴AE:DF=AD:MF,即t:$\frac{2}{t}$=$\frac{2}{t}$:2t,即t2=$\sqrt{2}$,
图中阴影部分的面积S=$\frac{1}{2}$•t•t+$\frac{1}{2}$•$\frac{2}{t}$•$\frac{2}{t}$=$\frac{1}{2}\sqrt{2}$+$\frac{1}{2}×$$\frac{4}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了反比例函数综合题,涉及到从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
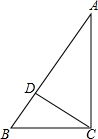 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$,请判断△ABC的形状,并说明理由.
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$,请判断△ABC的形状,并说明理由. 如图,a、b为实数,化简|a+b|=-a-b.
如图,a、b为实数,化简|a+b|=-a-b.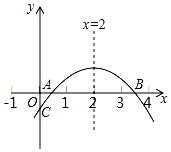 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论: 如图,AB∥CD,BC平分∠ACD,若∠1=54°,则∠2=63°.
如图,AB∥CD,BC平分∠ACD,若∠1=54°,则∠2=63°.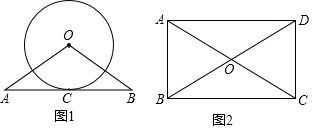
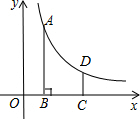 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )