题目内容
20．若函数y=kx+2的图象与x轴、y轴的交点之间的距离为$\sqrt{5}$，则k的值为2或-2．分析 根据题意画出图形，进而得出图象与y轴交点坐标，再利用勾股定理得出BO，OB′的长，进而求出k的值．
解答 
解：如图所示：
∵函数y=kx+2，
∴图象与y轴的交点坐标为：（0，2），则OA=2，
∵图象与x轴、y轴的交点之间的距离为$\sqrt{5}$，
∴AB=AB′=$\sqrt{5}$，
∴BO=OB′=1，
∴B（-1，0），B′（1，0），
分别代入y=kx+2得：
0=-k+2，0=k+2，
解得：k=2或-2．
故答案为：2或-2．
点评 此题主要考查了一次函数图象上点的坐标特征，正确得出图象与x轴的交点坐标是解题关键．
练习册系列答案
相关题目
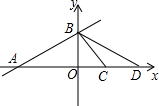已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴，y轴，分别交于A、B两点，点C坐标为（1，0），点D在x轴上，且∠BCD和∠ABD是两个不相等的钝角，求经过B、D两点的一次函数的解析式．
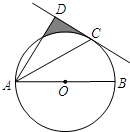如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．若AB=$2\sqrt{6}$，∠BAC=30°，则图中阴影部分的面积为$\frac{9\sqrt{3}}{4}$-π．
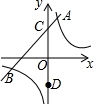如图，一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A，B两点，与y轴交于点C，C点关于x轴的对称点是D点，则△ABD的面积是15．