题目内容
6. 如图,已知AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F,OE=OF,求证:AB=CD.
如图,已知AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F,OE=OF,求证:AB=CD.
分析 如图,首先由垂径定理可得AE=BE,CF=DF;要证明AB=CD,只要证明BE=DF即可;观察发现△OBE≌△ODF,得到BE=DF,即可解决问题.
解答  解:如图,∵OE⊥AB,OF⊥CD,
解:如图,∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF;在△OBE与△ODF中,
$\left\{\begin{array}{l}{OB=OD}\\{OE=OF}\end{array}\right.$,
∴△OBE≌△ODF(HL),
∴BE=DF,2BE=2DF,
即AB=CD.
点评 该题主要考查了垂径定理、全等三角形的判定等几何知识点及其应用问题;牢固掌握垂径定理、全等三角形的判定是基础,灵活运用、解题是关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15.一个水池有甲、乙两个进水管,单独开甲、乙管各需要x小时、y小时可注满水池,现两管同时打开,则注满空池的时间为( )
| A. | $\frac{x+y}{xy}$小时 | B. | $\frac{xy}{x+y}$小时 | C. | $\frac{1}{x+y}$小时 | D. | $\frac{1}{xy}$小时 |
 如图,直线1与反比例函数y=$\frac{2}{x}$的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为$\frac{{m}^{2}-1}{m}$.
如图,直线1与反比例函数y=$\frac{2}{x}$的图象在第一象限内交于A,B两点,交x轴于点C,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为$\frac{{m}^{2}-1}{m}$.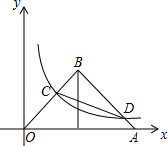 如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°.
如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°.
 用8块相同的长方形地砖拼成一块巨型地面,地砖的拼放方式及相关数据如图所示,利用所学知识求每块地砖的长和宽.
用8块相同的长方形地砖拼成一块巨型地面,地砖的拼放方式及相关数据如图所示,利用所学知识求每块地砖的长和宽.