题目内容
5.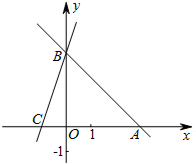 直线AB:y=-x+b分别与x,y轴交于A,B两点,点A的坐标为 (3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A,B两点,点A的坐标为 (3,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.(1)求点B的坐标及直线BC的解析式;
(2)在x轴上方存在点D,使以点A,B,D为顶点的三角形与△ABC全等,画出△ABD并请直接写出点D的坐标;
(3)在线段OB上存在点P,使点P到点B,C的距离相等,求出点P的坐标.
分析 (1)先把A点坐标代入y=-x+b可计算出b=3,即可得到C点坐标,进而得出直线BC的解析式;
(2)点A,B,D为顶点的三角形与△ABC全等得出点D的坐标;
(3)设PB=PC=x,根据勾股定理解答即可.
解答 解:(1)把A (3,0)代入y=-x+b,得 b=3,
∴B(0,3),
∴OB=3,
∵OB:OC=3:1,
∴OC=1,
∵点C在x轴负半轴上,
∴C(-1,0),
设直线BC的解析式为y=mx+n,
把B(0,3)及C(-1,0)代入,得$\left\{\begin{array}{l}n=3\\-m+n=0\end{array}\right.$,
解得 $\left\{\begin{array}{l}m=3\\ n=3\end{array}\right.$.
∴直线BC的解析式为:y=3x+3;
(2)如图,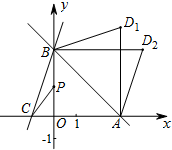
进而得出D1(4,3),D2(3,4);
(3)由题意,PB=PC,
设PB=PC=x,则OP=3-x,
在Rt△POC中,∠POC=90°,
∴OP2+OC2=PC2,
∴(3-x)2+12=x2,
解得,x=$\frac{5}{3}$,
∴OP=3-x=$\frac{4}{3}$,
∴点P的坐标(0,$\frac{4}{3}$).
点评 本题考查了一次函数的综合题,关键是利用两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式解答.

练习册系列答案
相关题目
20.下列因式分解中,正确的是( )
| A. | ax2-ax=x(ax-a) | B. | a2b2+ab2c+b2=b2(a2+ac+1) | ||
| C. | x2-y2=(x-y)2 | D. | x2-5x-6=(x-2)(x-3) |
14.下列说法中,错误的是( )
| A. | 两点之间的所有连线中,线段最短 | B. | 经过两点有且只有一条直线 | ||
| C. | 射线AB和射线BA是同一条射线 | D. | 线段AB和线段BA是同一条线段 |
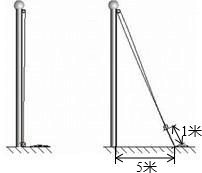 如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米,请算出旗杆的高度.
如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米,请算出旗杆的高度. 如图,△ABC≌△ADE,且∠EAB=120°,∠B=30°,∠CAD=10°,则∠CFA=85°.
如图,△ABC≌△ADE,且∠EAB=120°,∠B=30°,∠CAD=10°,则∠CFA=85°. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.