题目内容
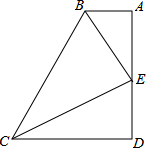 如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由.
如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由.考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:延长BE交CD的延长线于点F,首先证明CF=BC,再根据等腰三角形的性质可得BE=EF,然后证明△ABE≌△FDE,进而得到FD=AB,再利用等量代换可得BC=AB+DC.
解答:解:BC=AB+CD成立,
理由如下:
延长BE交CD的延长线于点F,
∵BE平分∠ABC,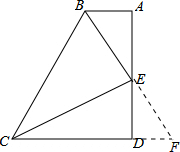
∴∠ABE=∠CBE,
∵AB∥CD,
∴∠F=∠ABE,∠A=∠FDA,
∴∠F=∠CBE,
∴CF=BC,
∵CE平分∠BCD,
∴BE=EF(三线合一)),
在△ABE和△DFE中,
,
∴△ABE≌△FDE(ASA),
∴FD=AB,
∵CF=DF+CD,
∴CF=AB+CD,
∴BC=AB+CD.
理由如下:
延长BE交CD的延长线于点F,
∵BE平分∠ABC,

∴∠ABE=∠CBE,
∵AB∥CD,
∴∠F=∠ABE,∠A=∠FDA,
∴∠F=∠CBE,
∴CF=BC,
∵CE平分∠BCD,
∴BE=EF(三线合一)),
在△ABE和△DFE中,
|
∴△ABE≌△FDE(ASA),
∴FD=AB,
∵CF=DF+CD,
∴CF=AB+CD,
∴BC=AB+CD.
点评:此题主要考查了全等三角形的判定与性质,证明三角形全等是证明线段相等的重要手段.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
若
+|b-1|=0,a2012+b2012的值为( )
| a+1 |
A、
| ||
| B、0 | ||
| C、2 | ||
| D、-2 |
下列结论一定正确的是( )
| A、两数的差一定小于被减数 |
| B、互为相反数两数差为0 |
| C、一个数减去0的结果为0 |
| D、0减去一个有理数的结果是这个有理数的相反数 |
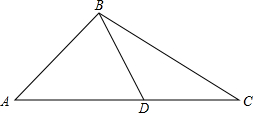 如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数.
如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数. 如图,有一圆柱形杯子高为15cm,放进长为30cm的吸管,已知吸管在杯子外的部分长5cm,求杯子的容积.
如图,有一圆柱形杯子高为15cm,放进长为30cm的吸管,已知吸管在杯子外的部分长5cm,求杯子的容积.