题目内容
已知等腰三角形的周长为27,一腰上的中线把三角形分为两个三角形,两个三角形的周长的差是3,求等腰三角形各边的长.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:根据题意画出图形,设等腰三角形的腰长为x,则底边长为27-2x,再根据两个三角形的周长差是3求出x的值即可.
解答:解 :如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,
:如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,
∵点D为AC的中点,
∴AD=CD=
,BC=27-(AB+AC)=27-2x.
①当△ABD的周长大于△BCD的周长时,
∵AB+AD+BD-(BC+CD+BD)=3,
∴AB-BC=3,
即x-(27-2x)=3,
解得x=10,
27-2x=7,
10,10,7能够组成三角形,符合题意;
②当△BCD的周长大于△ABD的周长时,
∵BC+CD+BD-(AB+AD+BD)=3,
∴BC-AB=3,
即27-2x-x=3,
解得x=8,
27-2x=11,
8,8,11能够组成三角形,符合题意.
综上所述,这个等腰三角形的腰长为10,底边长为7或腰长为8,底边长为11.
 :如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,
:如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,∵点D为AC的中点,
∴AD=CD=
| 1 |
| 2 |
①当△ABD的周长大于△BCD的周长时,
∵AB+AD+BD-(BC+CD+BD)=3,
∴AB-BC=3,
即x-(27-2x)=3,
解得x=10,
27-2x=7,
10,10,7能够组成三角形,符合题意;
②当△BCD的周长大于△ABD的周长时,
∵BC+CD+BD-(AB+AD+BD)=3,
∴BC-AB=3,
即27-2x-x=3,
解得x=8,
27-2x=11,
8,8,11能够组成三角形,符合题意.
综上所述,这个等腰三角形的腰长为10,底边长为7或腰长为8,底边长为11.
点评:本题考查的是等腰三角形的性质,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四边形ABCD中,AB=2
如图,在四边形ABCD中,AB=2| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
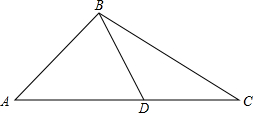 如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数.
如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数. 如图所示,M是弧AB的中点,OM是⊙O 半径交弦AB于点N,AB=4
如图所示,M是弧AB的中点,OM是⊙O 半径交弦AB于点N,AB=4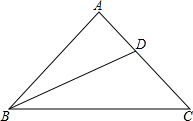 如图,在Rt△ABC中,∠A=90°,BD是角平分线,且BC=AB+AD,求证:AB=AC.
如图,在Rt△ABC中,∠A=90°,BD是角平分线,且BC=AB+AD,求证:AB=AC. 八年级(2)班为了正确引导学生树立正确的消费观,随机调查了10名同学某日的零花钱情况,其统计图表如下:
八年级(2)班为了正确引导学生树立正确的消费观,随机调查了10名同学某日的零花钱情况,其统计图表如下: