Question

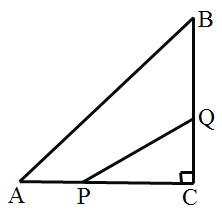
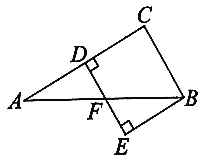
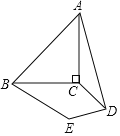
【题目】如图，等腰直角三角形ABC的斜边AB＝，将线段AB绕着点A逆时针旋转60°，点B的对应点为D，连接CD，将线段CD绕点D逆时针旋转60°，点C的对应点为E，连接BE，则∠ABE＝_____°．

Answer 1

【答案】75

【解析】

由旋转的性质可得AB＝AD，∠BAD＝60°，CD＝DE，∠CDE＝60°，由“SSS”可证△BCD≌△ACD，可得∠ADC＝∠BDC＝30°，∠ACD＝∠BCD＝135°，由三角形内角和可得∠CBD＝15°，由“SAS”可证△BCD≌△BED，可得∠EBD＝∠CBD＝15°，即可求解．

连接BD，

∵将线段AB绕着点A逆时针旋转60°，

∴AB＝AD，∠BAD＝60°，

∴△ABD是等边三角形，

∴AB＝AD＝BD，∠ADB＝60°＝∠ABD，

∵AD＝BD，BC＝AC，CD＝CD，

∴△BCD≌△ACD（SSS）

∴∠ADC＝∠BDC＝30°，∠ACD＝∠BCD＝＝135°，

∴∠CBD＝15°，

∵将线段CD绕点D逆时针旋转60°，

∴CD＝DE，∠CDE＝60°，

∴∠CDB＝∠BDE＝30°，且BD＝BD，CD＝ED，

∴△BCD≌△BED（SAS）

∴∠EBD＝∠CBD＝15°，

∴∠ABE＝∠ABD+∠EBD＝75°，

故答案为：75．