题目内容
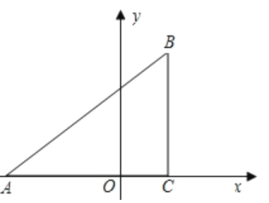
【题目】如图,反比例函数y=![]() (k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(
(k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(![]() ,6),且E为BC的中点,D为x轴负半轴上的点.
,6),且E为BC的中点,D为x轴负半轴上的点.

(1)求反比倒函数的表达式和点F的坐标;
(2)若D(﹣![]() ,0),连接DE、DF、EF,则△DEF的面积是 .
,0),连接DE、DF、EF,则△DEF的面积是 .
【答案】(1)y=![]() ,F(3,3);(2)S△DEF=9.
,F(3,3);(2)S△DEF=9.
【解析】
(1)利用待定系数法即可求得反比例函数的解析式,根据题意求得B的坐标,进而得到F的横坐标,代入解析式即可求得纵坐标;
(2)设DE交y轴于H,先证得H是OC的中点,然后根据S△DEF=S矩形OABC+S△ODH﹣S△ADF﹣S△CEH﹣S△BEF即可求得.
(1)∵反比例函数y=![]() (k≠0,x>0)的图象过E(
(k≠0,x>0)的图象过E(![]() ,6),
,6),
∴k=![]() ×6=9,
×6=9,
∴反比例函数的解析式为y=![]() ,
,
∵E为BC的中点,
∴B(3,6),
∴F的横坐标为3,
把x=3代入y=![]() 得,y=
得,y=![]() =3,
=3,
∴F(3,3);
(2)设DE交y轴于H,
∵BC∥x轴,
∴△DOH∽△ECH,
∴![]() =
=![]() =1,
=1,
∴OH=CH=3,
∴S△DEF=S矩形OABC+S△ODH﹣S△ADF﹣S△CEH﹣S△BEF=3×6+![]() ×
×![]() ×3﹣
×3﹣![]() ×(3+
×(3+![]() )×3﹣
)×3﹣![]() ﹣
﹣![]() =9.
=9.
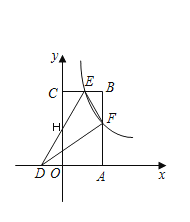

练习册系列答案
相关题目