Question

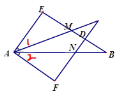
【题目】已知：如图，AC=CB，DA=DB，AE=2DE，BF=2DF．

求证：（1）∠A=∠B；（2）CE=CF

Answer 1

【答案】（1）见解析；(2)见解析.

【解析】

（1）由“AC=CB，DA=DB”结合图形特点，连接CD即可证得△ACD≌△BCD，从而得出答案；（2）结合（1）与“AE=2DE，BF=2DF”可知AE=BF，从而可证△ACE≌△BCF，从而可得出答案

解：（1）连结 CD，

在△ADC 和△BDC 中

∵AC=CB，DA=DB，DC=DC，

∴△ADC≌△BDC(SSS)，

∴∠A=∠B．

（2）∵DA=DB，AE=2DE，BF=2DF，

∴AE= AD ，BF= BD ，

∴AE=BF．

在△AEC和△BFC 中

∵AC=CB，∠A=∠B，AE=BF，

∴△AEC≌△BFC(SAS)，

∴CE=CF．