题目内容
12．因式分解：（1）（a2+b2）2-4a2b2；
（2）（m2-m）2+$\frac{1}{2}$（m2-m）+$\frac{1}{16}$．
分析 （1）首先利用平方差公式分解因式，进而利用完全平方公式分解因式得出即可；
（2）直接利用完全平方公式分解因式，进而再次利用完全平方公式分解因式．
解答 解：（1）（a2+b2）2-4a2b2
=（a2+b2+2ab）（a2+b2-2ab）
=（a+b）2（a-b）2；
（2）（m2-m）2+$\frac{1}{2}$（m2-m）+$\frac{1}{16}$
=（m2-m+$\frac{1}{4}$）2，
=（m-$\frac{1}{2}$）4．
点评 此题主要考查了公式法分解因式，熟练应用乘法公式是解题关键．
练习册系列答案
相关题目
17．下列调查，样本具有代表性的是（ ）
| A． | 了解全校同学对课程的喜欢情况，对某班男同学进行调查 | |
| B． | 了解某小区居民的防火意识，对你们班同学进行调查 | |
| C． | 了解商场的平均日营业额，选在周末进行调查 | |
| D． | 了解观众对所看电影的评价情况，对座号是奇数号的观众进行调查 |
1．
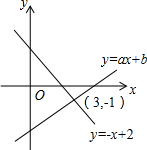如图，直线y=-x+2与y=ax+b（a≠0且a，b为常数）的交点坐标为（3，-1），则关于x的不等式-x+2≥ax+b的解集为（ ）
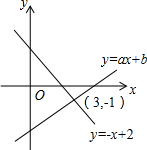如图，直线y=-x+2与y=ax+b（a≠0且a，b为常数）的交点坐标为（3，-1），则关于x的不等式-x+2≥ax+b的解集为（ ）| A． | x≥-1 | B． | x≥3 | C． | x≤-1 | D． | x≤3 |
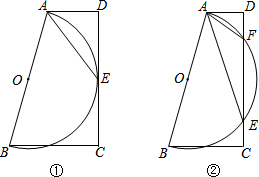在梯形ABCD中，AD∥BC，∠D=90°，以AB为直径作⊙O．