题目内容
1.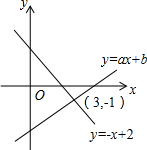 如图,直线y=-x+2与y=ax+b(a≠0且a,b为常数)的交点坐标为(3,-1),则关于x的不等式-x+2≥ax+b的解集为( )
如图,直线y=-x+2与y=ax+b(a≠0且a,b为常数)的交点坐标为(3,-1),则关于x的不等式-x+2≥ax+b的解集为( )| A. | x≥-1 | B. | x≥3 | C. | x≤-1 | D. | x≤3 |
分析 函数y=-x+2与y=ax+b(a≠0且a,b为常数)的交点坐标为(3,-1),求不等式-x+2≥ax+b的解集,就是看函数在什么范围内y=-x+2的图象对应的点在函数y=ax+b的图象上面.
解答 解:从图象得到,当x≤3时,y=-x+2的图象对应的点在函数y=ax+b的图象上面,
∴不等式-x+2≥ax+b的解集为x≤3.
故选D.
点评 本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
相关题目
16.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
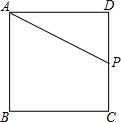 如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.
如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.