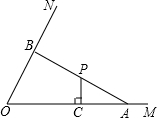
题目内容
已知tan∠AOB=
,P、Q分别是射线OA、OB上的两个动点(都不与O点重合),则
的最小值是
.
| 2 |
| 3 |
| PQ |
| OQ |
2
| ||
| 13 |
2
| ||
| 13 |
分析:构造Rt△AOB,使∠A=90°,tan∠AOB=
,那么当OQ越大并且OQ越小时,
有最小值,那么当Q运动到B点时,过B作OA的垂线段,垂足为P,此时P与A重合,即可求解.
| 2 |
| 3 |
| PQ |
| OQ |
解答:解:如图, Rt△AOB中,∠A=90°,tan∠AOB=
Rt△AOB中,∠A=90°,tan∠AOB=
,
设AB=2k,OA=3k,
由勾股定理,得OB=
=
k.
当Q运动到B点时,过B作OA的垂线段,垂足为P,此时P与A重合,
有最小值,
所以
=
=
=
.
故答案为
.
 Rt△AOB中,∠A=90°,tan∠AOB=
Rt△AOB中,∠A=90°,tan∠AOB=| 2 |
| 3 |
设AB=2k,OA=3k,
由勾股定理,得OB=
| AB2+OA2 |
| 13 |
当Q运动到B点时,过B作OA的垂线段,垂足为P,此时P与A重合,
| PQ |
| OQ |
所以
| PQ |
| OQ |
| AB |
| OB |
| 2k | ||
|
2
| ||
| 13 |
故答案为
2
| ||
| 13 |
点评:本题考查了锐角三角函数的定义,解直角三角形,有一定难度,确定动点P、Q的位置是解题的关键.

练习册系列答案
相关题目
 长线上一点,连接AP并延长与射线ON交于点B.
长线上一点,连接AP并延长与射线ON交于点B. 如图,已知Rt△AOB的锐角顶点A在反比例函数y=
如图,已知Rt△AOB的锐角顶点A在反比例函数y= (a≠
(a≠ 0,m≠0)交于A、D两点,已知tan∠AOB=
0,m≠0)交于A、D两点,已知tan∠AOB= ,三角形ABO的面积S△ABO=
,三角形ABO的面积S△ABO= .
. ,P、Q分别是射线OA、OB上的两个动点(都不与O点重合),则
,P、Q分别是射线OA、OB上的两个动点(都不与O点重合),则 的最小值是________.
的最小值是________.